Problem 1

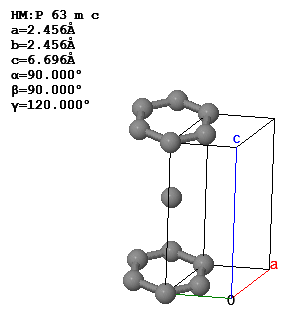
The conventional unit cell and lattice parameters of graphite are shown to the right.

(a) What is the Bravais lattice of graphite?

(b) How many symmetry elements are there in the point group of graphite?

(c) Find the electronic band structure of graphite online and sketch the bands near the chemical potential.

(d) Explain how you can tell from the bandstructure if graphite is a metal, a semiconductor, or an insulator.

Problem 2

(a) How may phonon normal modes are there in 1 cm³ of graphite?

(b) How can you estimate the thermal conductivity of a metal if you know the electrical conductivity?

(c) Why does the phonon dispersion relation for silver look like the phonon dispersion relation for copper? Name another material with a similar phonon disperion as copper.

(d) If you knew the phonon density of states for copper and quarz (SiO₂), you could calculate the specific heat of quarz but not copper. Why?

Problem 3
Germanium is an indirect semiconductor with a bandgap of 0.67 eV. The valence band maximum is at $k = 0$ but the conduction band minimum is in the <111> direction.

(a) What is the chemical potential for intrinsic Ge measured from the top of the valence band at 300 K? (The top of the valence band is defined to have an energy of zero.)

(b) Draw the electron density of states for Ge as a function of energy near the top of the valence band and the bottom of the conduction band.

(c) What is the concentration of electrons in the conduction band of intrinsic silicon at 300 K?

Problem 4

(a) Using the empty lattice approximation, draw the electronic band structure of a bcc metal.

(b) This metal has two valence electrons per unit cell. Include the Fermi energy in your drawing.

(c) $E=0$ is indicated in the plot. What is approximately the Fermi energy in electron volts if the lattice constant (= side of the conventional unit cell) is $a=4.3$ Å? (You can estimate $E_F$ if you calculate the energies where the dispersion curve meets the Brillouin zone boundaries.)

(d) What phonon mode has the shortest wavelength in this bcc crystal? Hint: $\overline{\Gamma N} < \overline{\Gamma P} < \overline{\Gamma H}$.