Problem 1

Consider a body centered cubic crystal with one atom in the basis. The length of a side of the conventional unit cell is called the lattice constant $a=$ 2 Å.

(a) What is the volume of the primitive unit cell?

(b) Draw the arrangement of the atoms in the (110) plane.

(c) What is the shape of the Wigner-Seitz cell for this bcc crystal?

(d) Give and example of a symmetry of the bcc crystal. Write the symmetry as a matrix if you can.

Problem 2

(a) For the bcc crystal in problem 1, the reciprocal lattice vectors are indexed using the conventional (cubic) primitive lattice vectors. What is the length of the reciprocal lattice vector $|\vec{G}_{112}|$?

(b) Draw the phonon dispersion relation for this bcc crystal along $P-\Gamma-H$.    $\overline{\Gamma P}=\frac{\sqrt{3}\pi}{a},\,\overline{\Gamma H}=\frac{2\pi}{a}.$

(c) How may phonon normal modes are there in 1 cm³ of the bcc crystal?

(d) X-rays with a wavelength of 1.5 Å are used in a diffraction experiment. What is the largest reciprocal lattice vector that can be measured with these x-rays?

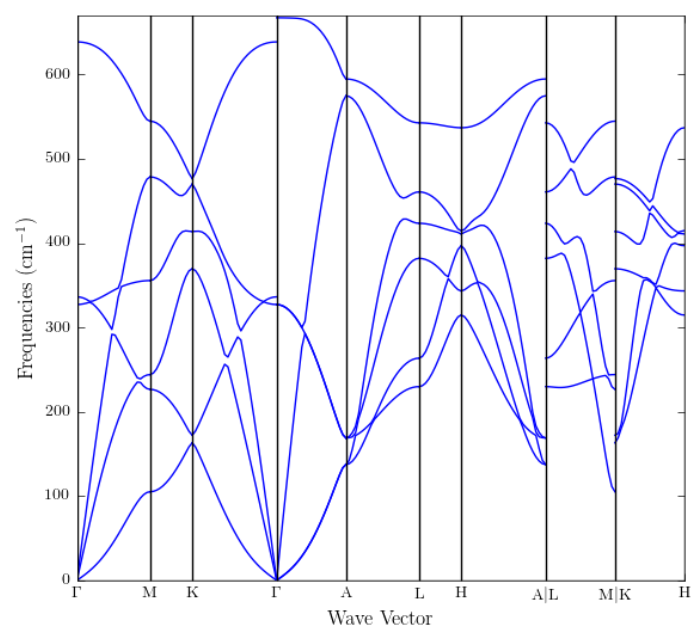
Problem 3

A phonon dispersion relation is shown below.

(a) How many atoms are there in the basis of this crystal?

(b) What is the highest frequency phonon mode in Hz?

(c) Label the Transverse Acoustic (TA) and the Longitudinal Acoustic (LA) modes in the $\Gamma -A$ directionand state how many Transverse Acoustic modes and how many Longitudinal Acoustic modes for every $\vec{k}$-value are there.

(d) What is the mean number of phonons in a phonon mode with an energy of 1 meV at 300 K?

Problem 4

An electron band structure is shown below. The bands with energies above $E =0$ are empty and the bands with energies less than $E =0$ are occupied.

(a) Is this material a metal, a semiconductor, or an insulator?

(b) What is the chemical potential of this material?

(c) Does this material have a direct band gap?

(d) Estimate the ratio of the heavy hole mass to the light hole mass, $m_{hh}/m_{lh}$.