Each subsections (a), (b), (c), $\cdots$ can be awarded a maximum of 10 points.
Problem 1
(a) If space group symmetries of a crystal are known, what can that tell you about the properties of the crystal?
(b) Give an example of a symmetry of a hexagonal crystal.
(c) What is the angle between the [100] direction and the [010] direction in a hexagonal lattice? What is the angle between the [100] direction and the [001] direction in a hexagonal lattice?
(d) How can you construct the primitive unit cell and the conventional unit cell of a crystal from the asymmetric unit and the space group?
Solution
Problem 2
You are given a crystal of some unkown material and are asked to determine the crystal structure using x-ray diffraction.
(a) Explain how you can measure the reciprocal lattice vectors in an x-ray diffraction experiment.
(b) Explain how you can determine the primitive reciprocal lattice vectors from the measured reciprocal lattice vectors.
(c) Explain how you can determine the real space primitive lattice vectors from the primitive reciprocal lattice vectors.
(d) Explain how you can determine the volume of the primitive unit cell from the real space lattice vectors.
(e) Explain how you can determine the arrangement of the atoms in the basis.
Solution
Problem 3
The Bravais lattice of NaCl is fcc and there are two atoms in the primitive unit cell (One Na atom and one Cl atom). The lattice constant of the conventional unit cell is 5.639 Å.
(a) How many acoustic branches and how many optical branches does the phonon dispersion of NaCl have?
(b) How many phonon modes does 1 cm³ of NaCl have?
(c) What is the mean number of phonons at 300 K in a phonon mode with an energy of 0.001 eV?
(d) How can you determine the speed of sound in a material from the phonon dispersion?
Solution
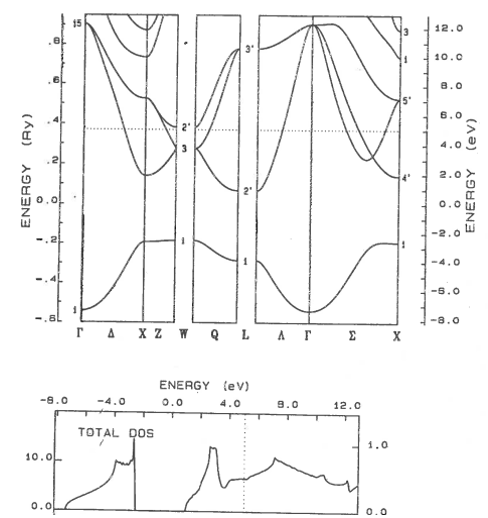
Problem 4
The band structure of some crystal is shown below. The dotted line is the Fermi energy.

(a) Is this material a metal, a semimetal, a semiconductor, or an insulator? Explain your reasoning.
(b) What experiments could be performed to verify this calculated band structure?
(c) What properties of this crystal could be calculated using the information given in this plot?
Solution