MAS.020 Introduction to Solid State Physics
31.01.2024

Name Matrikelnr.

Each subsections (a), (b), (c), $\cdots$ can be awarded a maximum of 10 points.

Problem 1

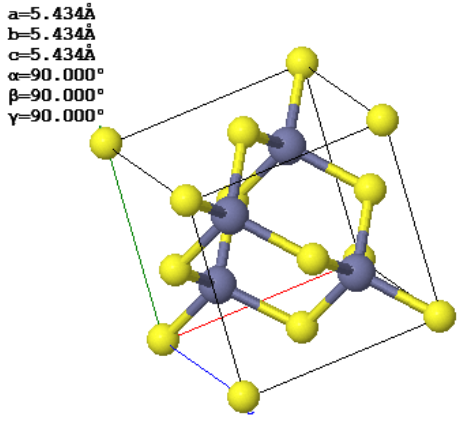
The conventional unit cell and the lattice parameters of a crystal are shown to the right.

(a) What is the Bravais lattice of this crystal?

(b) How many atoms are there in the primitive unit cell of this crystal?

(d) Circle a purple atom and a yellow atom in the drawing. Specify the direction from the yellow atom to the purple atom using Miller indicies.

Solution

Problem 2

(a) Many properties of solids are described by tensors. Give an example of a rank one tensor, a rank two tensor, a rank three tensor, and a rank four tensor.

(b) Three-dimensional periodic functions can be described by a Fourier series. Consider the function $\exp(i(3x + 4y+ 6z))$. Since this is a 3-D periodic function, you can define three primitive lattice vectors for it. What are the primitive lattice vectors for this function?

      Aluminum
      CELL PARAMETERS:    4.0496   4.0496   4.0496   90.000   90.000   90.000
      SPACE GROUP: Fm3m      
      X-RAY WAVELENGTH:     1.541838
      Cell Volume:     66.409
      Density (g/cm3):      2.698
      MAX. ABS. INTENSITY / VOLUME**2:      34.61439413    
      RIR:      4.177
      RIR based on corundum from Acta Crystallographica A38 (1982) 733-739
               2-THETA      INTENSITY    D-SPACING   H   K   L   Multiplicity
                38.50        100.00        2.3380    1   1   1         8
                44.76         47.49        2.0248    2   0   0         6
                65.16         28.01        1.4317    2   2   0        12
                78.30         30.71        1.2210    3   1   1        24
                82.52          8.74        1.1690    2   2   2         8
================================================================================

What do the columns 2-THETA, INTENSITY, D-SPACING, H K L, mean?

(d) Based on the powder diffraction data, determine the primitive reciprocal lattice vectors for aluminum.

Solution

(a) Rank 1: pyroelectricity and pyromagnetism 
Rank 2: electrical conductivity, thermal conductivity, dielectic constant, magnetic susceptibility, and thermal expansion 
Rank 3: piezoelectricity and piezomagnetism 
Rank 4: stiffness, piezoconductivity

(b) This function has a periodicity of $2\pi/3$ in the $x-$direction, $2\pi/4$ in the $y-$direction, and $2\pi/6$ in the $z-$direction.
Primitive lattice vectors would be 
$$\vec{a}_1 = \frac{2\pi}{3} \hat{x}$$ 
$$\vec{a}_2 = \frac{2\pi}{4} \hat{y}$$ 
$$\vec{a}_3 = \frac{2\pi}{6} \hat{z}$$

(c) There is a diffraction peak when $\vec{k}' - \vec{k} =\vec{G}$ where $\vec{G}$ is one of the reciprocal lattice vectors. 2-THETA is the angle between $\vec{k}'$ and $\vec{k}$, INTENSITY is the intensty of the diffraction peak normalized to the peak with the smallest D-Spacing, D-SPACING is the distance between the net planes $=\frac{2\pi}{|\vec{G}|}$ (this is not necessarily the distance between atomic planes), H K L are the reciprocal lattice vector labels $\vec{G}_{HKL} = H\vec{b}_1 +K\vec{b}_2 +L\vec{b}_3$, Multiplicity is the number of reciprocal lattice vectors with the same D-SPACING.

(d) You can define primitive reciprocal lattice vectors for the conventional unit cell or the primitive unit cell. Diffraction data for cubic crystals is normally given in terms of the conventional unit cell (although an answer in terms of the primitive unit cell would also be correct.) Since the lattice constant is given as 4.0496 Å, the primitive reciprocal lattice vectors are,

$\vec{b}_1 = \frac{2\pi}{4.0496} = 1.55 \hat{x}$ Å-1
$\vec{b}_2 = \frac{2\pi}{4.0496} = 1.55 \hat{y}$ Å-1
$\vec{b}_3 = \frac{2\pi}{4.0496} = 1.55 \hat{z}$ Å-1

Problem 3

(a) What determines the number of phonon modes in a crystal?

(b) What determines the average number of phonons in a phonon mode?

(c) Why is the calculation of the specific heat for insulators different from the calculation of the specific heat for metals?

(d) Two materials have the same crystal structure. What does this tell you about the phonon density of states of the two materials?

Solution

Problem 4

InSb is a direct band gap semiconductor with a band gap of $E_g = 0.17$ eV. The minimum of the conduction band is at the $\Gamma$-point. The effective mass of the electrons is $m_e = 0.014m_0$, the effective mass of the light holes is $m_{lh} = 0.015m_0$, and the effective mass of the heavy holes is $m_{hh} = 0.435m_0$ where $m_0= 9.1093837015\times 10^{-31}$ kg is the mass of an electron.

(a) Sketch the band diagram of InSb.

(b) Sketch the electron density of states of InSb.

(d) For which wavelengths of light is InSb is transparent?

Solution

MAS.020 Introduction to Solid State Physics 31.01.2024

MAS.020 Introduction to Solid State Physics
31.01.2024