Problem 1

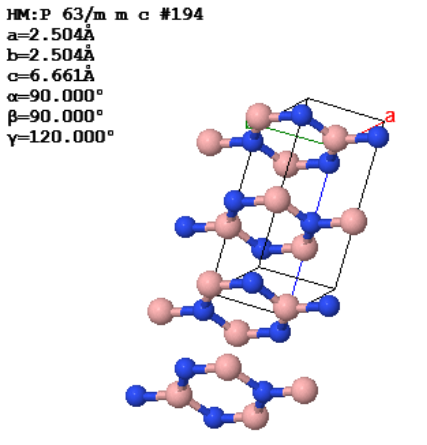
The conventional unit cell and the lattice parameters of a crystal are shown to the right.

(a) What is the Bravais lattice of this crystal?

(b) What experiment could you perform to determine how many atoms there are in a primitive unit cell?

(c) What is the volume of the primitive unit cell?

(d) How could you find the space group and the point group of this crystal?

Solution

Problem 2

Polonium is the only element that forms a simple cubic crystal structure. The lattice constant is $a = 3.359$ Å.

(a) Calculate the primitive reciprocal space lattice vectors.

(b) Calculate the length of the reciprocal lattice vector $\vec{G}_{322} (h =3,\, k = 2,\, l =2)$. Give the units in your answer.

(c) At which scattering angle 2θ is the diffraction of the 322 reflection is observed, if the wavelength of the X-rays is 1.0 Å?

(d) What is the smallest reciprocal lattice vector of this crystal?

Solution

Problem 3

(a) A crystal has 4 atoms in the primitive unit cell. The whole crystal contains $N$ atoms. How many phonon modes are there?

(b) How many of the phonon modes from (a) are acoustic modes?

(c) How could you calculate the phonon contribution to the specific heat of this crystal?

(d) What other property besides the specific heat can you calculate from the phonon density of states?

Solution

Problem 4

The electronic band structure of a material is shown below.

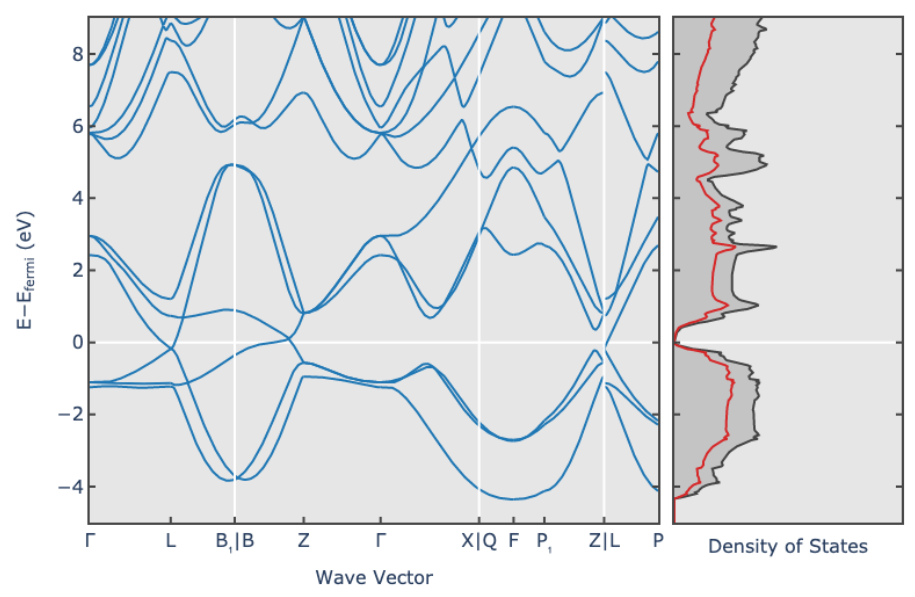
(a) Is this material a metal, a semiconductor, or an insulator? Explain your reasoning.

(b) What does this data tell you about the electrical conductivity and thermal conductivity of this material?

(c) $f(\vec{r})$ is a three-dimensional periodic function. How can you write this function as a Fourier series?

(d) Why is the electric susceptibility a symmetric matrix?

Solution