Optical Instruments

Many simple optical instruments (such as microscopes and telescopes) are constructed from two lenses. In this app the light rays travel from left to right. Here $f_L$ is the focal length of the left lens, $f_R$ is the focal of the right lens, $L$ is the distance between the lenses, $x_o$ is the distance from the object to the left lens, $x_i$ is the distance from the right lens to the image, $y_o$ is the distance of the object from the optical axis, and $y_i$ is the distance from the image to the optical axis. The small divisions along the optical axis are mm.

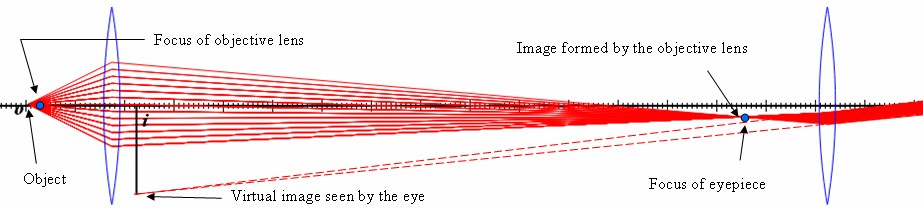
Microscope
A compound microscope consists of two lenses, the objective lens and the eyepiece. The object to be viewed is placed just beyond the focal length of the objective lens. This produces a real, inverted image far from the objective lens. This image is larger than the object. The eyepiece is placed about $1/f_{\text{eyepiece}}$ from this image. This bends the light rays so they are nearly parallel so they can be viewed by an eye. The eye sees a virtual image that appear much farther away than the image formed by the objective lens.

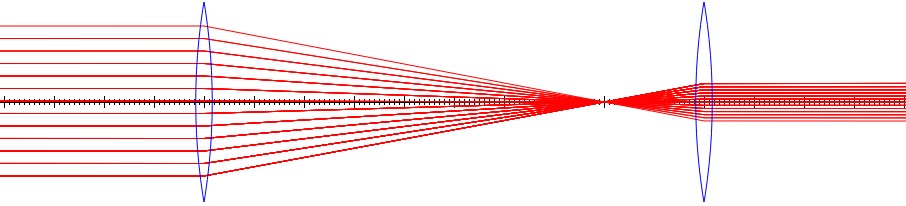
Keplerian telescope
For a telescope, the object is far away and the light rays entering the telescope are nearly parallel. These parallel rays form an image at the focal length of the objective lens. The eyepiece is then used to bend the light rays so that they are nearly parallel again so that they can be viewed by an eye. The length of the telescope is therefore about the sum of the two focal lengths. The magnification is ratio of the angle from the optical axis to the image $\theta_i=y_i/x_i$ to the angle between the optical axis and the object $\theta_o=y_o/x_o$, $m=\theta_i/\theta_o=\frac{y_i}{x_i}\frac{x_o}{y_o}$.

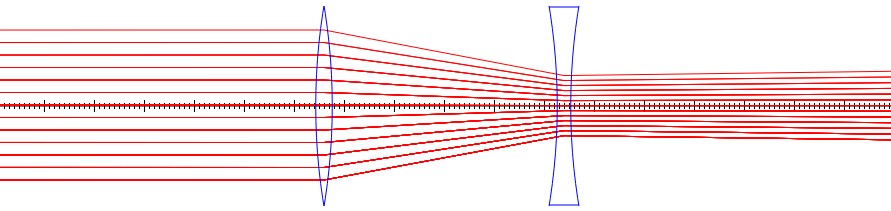
Galilean telescope
Galileo first built a telescope in 1609 and was able to achieve a magnification of about 30. He made observations of the moon and Jupiter's moons and published these in Sidereus Nuncius. The light rays entering the telescope are nearly parallel. These parallel rays would form an image at the focal length of the objective lens. Galileo used a diverging lens as an eyepiece which he placed before the focus of the objective lens to bend the rays parallel again so that they could be viewed by an eye. The magnification is ratio of the angle from the optical axis to the image $\theta_i=y_i/x_i$ to the angle between the optical axis and the object $\theta_o=y_o/x_o$, $m=\theta_i/\theta_o=\frac{y_i}{x_i}\frac{x_o}{y_o}$.