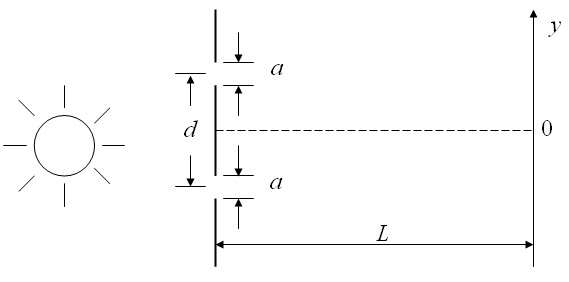
Diffraction by two slits of width a

Light falls on two slits of width $a$ which have a center-to-center spacing of $d$. An interference pattern is placed a distance $L$ from the slits and an interference pattern is observed on the screen. The double-slit interfernce pattern for narrow slits is modulated by the single-slit pattern.

$a=$

[m]

$d=$

[m]

$L=$

[m]

$\lambda=$

[nm]

The small divisions on the scale on the right represent mm.

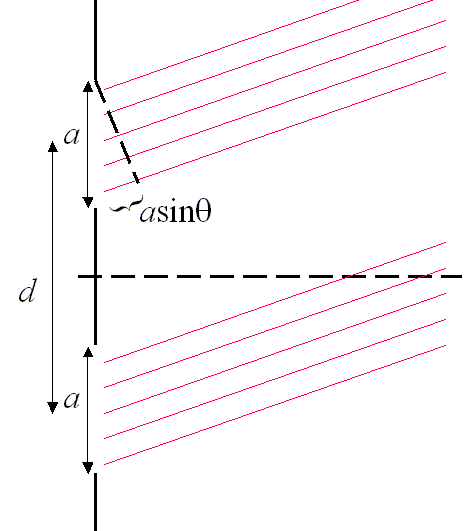
  Your browser does not support the canvas element.

Two slits separated by a distance $d$ that each have a width $a$ display a diffraction pattern that is a product of the double slit interference pattern and the single slit diffraction pattern. We define $\delta = 2\pi d\sin(\theta)/\lambda$ and $\beta = 2\pi a\sin(\theta )/\lambda$. To determine the total amplitude, we integrate over both slits.

\[ \begin{equation} \large A=\frac{A_0}{a}\int\limits_{-\frac{d}{2}-\frac{a}{2}}^{-\frac{d}{2}+\frac{a}{2}}\exp \left(i\omega t + i\frac{\beta y}{a}\right)dy+\frac{A_0}{a}\int\limits_{\frac{d}{2}-\frac{a}{2}}^{\frac{d}{2}+\frac{a}{2}}\exp \left(i\omega t + i\frac{\beta y}{a}\right)dy \end{equation} \]

Performing the integration gives,

\[ \begin{equation} \large A=\frac{A_0}{i\beta}e^{i\omega t} \left( e^{-i\frac{\delta}{2}}e^{i\frac{\beta}{2}} - e^{-i\frac{\delta}{2}}e^{-i\frac{\beta}{2}} +e^{i\frac{\delta}{2}}e^{i\frac{\beta}{2}} - e^{i\frac{\delta}{2}}e^{-i\frac{\beta}{2}} \right) \end{equation} \]

This can be written as,

\[ \begin{equation} \large A=\frac{A_0}{i\beta}e^{i\omega t} \left( e^{i\frac{\beta}{2}} - e^{-i\frac{\beta}{2}} \right)\left( e^{i\frac{\delta}{2}} + e^{i\frac{\delta}{2}} \right)=\frac{2A_0}{\beta/2}e^{i\omega t}\cos(\delta/2)\sin(\beta/2) \end{equation} \]

The intensity is proportional to the squared amplitude,

\[ \begin{equation} \large I=I_0\frac{\sin^2(\beta/2)}{(\beta/2)^2}\cos^2(\delta/2) \end{equation} \]
$\frac{I}{I_0}$

$y$