Double slit experiment
|
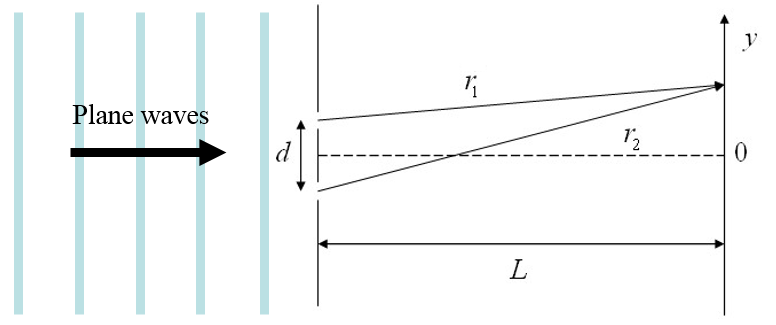
In a double slit experiment, waves pass through two narrow slits that are spaced a distance $d$ apart. The interference pattern is observed on a screen that is a distance $L$ from the slits.
|
Here $r_1$ is the distance from source 1 and $r_2$ is the distance from source 2 measured in centimeters. The wavenumber $k$ is related to the wavelength $\lambda$, $k=\frac{2\pi}{\lambda}$, and the angular frequency $\omega$ is related to the period $T$, $\omega=\frac{2\pi}{T}$.
The distances from the two sources to the point at height $y$ on the screen are,
$r_1 = \sqrt{L^2+(y-d/2)^2},$
$r_2 = \sqrt{L^2+(y+d/2)^2}.$
The waves leave the slits with the same amplitude $A$ and the same phase (which we choose to be zero). The waves interfere at the screen. The amplitude of the waves at the screen is,
$\frac{A}{\sqrt{r_1}} \exp (ikr_1)+\frac{A}{\sqrt{r_2}} \exp (ikr_2).$
The intensity is the square of the amplitude,
$\large I \propto \left(\frac{A}{\sqrt{r_1}} \cos(kr_1)+\frac{A}{\sqrt{r_2}} \cos(kr_2)\right)^2+\left(\frac{A}{\sqrt{r_1}} \sin(kr_1)+\frac{A}{\sqrt{r_2}} \sin(kr_2 )\right)^2.$
This is the exact result for the interference pattern. However, by making an approximation, it can be expressed in a simpler form. For $y < < L$, $A/\sqrt{r_1} \approx A/\sqrt{r_2} \approx A/\sqrt{L}$. Using the trigonometric identities, $\sin a+\sin b=2\sin ((a+b)/2)\cos ((a-b)/2)$ and $\cos a +\cos b=2\cos ((a+b)/2)\cos ((a-b)/2)$
$\large I \propto \frac{4A^2}{L} \left(\sin^2((kr_1+kr_2)/2)+\cos^2((kr_1+kr_2)/2)\right)\cos^2((kr_1-kr_2)/2).$
$\large I \propto \frac{4A^2}{L} \cos^2\left( \frac{kr_1-kr_2}{2}\right).$
$\large I \propto \frac{4A^2}{L} \cos^2\left( \frac{kdy}{2L}\right).$
| $\frac{I}{I_0}$ | |
$y$ |
Far field
In the far field, where $L > > \lambda$ and $L > > y$, constructive interference will take place when $n\lambda=yd/L$ where $n$ is an integer. Destructive interference will take place when $(n+1/2)\lambda=yd/L$.