Real and virtual images

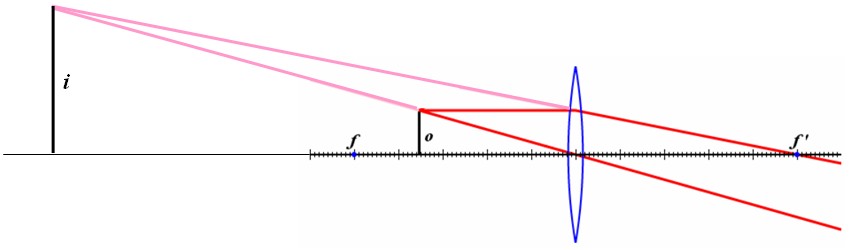
An object $o$ is placed a distance $x_o$ in front of a thin lens at $x=0$. The object is a distance $y_0$ from the optical axis. The image of this object $i$ appears at a distance $x_i$ behind the lens at a distance $y_i$ from the optical axis. There are three special rays that can be used to find the position of the image. The ray that leaves the object and travels parallel to the optical axis will be bent by the lens through the focal point on the far side of the lens. A ray that travels from the object through the focal point on the near side of the lens will be bent parallel to the optical axis on the far side of the lens. The ray that leaves the object and travels through the center of the lens is not bent. These three rays (drawn in red) all intersect at the image. The thin lens equation can be used to relate the distance from the lens to the object $x_o$ and the distance to the lens to the image $x_i$ to the focal length $f$. If the position of the lens is $x=0$ and $x_o < 0$, the thin lens formula is,

$\Large \frac{-1}{x_o}+\frac{1}{x_i}= \frac{1}{f}$.

An object placed further from a converging lens than the focal length will form an image on the opposite side of the lens. If a viewing screen is placed at the image position, the object will be seen in focus but upsidedown. This is a real, inverted image. The magnification is the height of the image divided by the height of the object. A bit of trigonometry shows that the magnification is, $m=y_i/y_o=f/(x_o+f)$. A negative magnification indicates that the image is inverted.

If the object is placed closer to a converging lens than the focal length, the rays on the far side of the lens diverge. By extrapolating these lines back (the pink lines) the position of virtual image can be found. On the far side of the lens it looks like the light is coming from the virtual image. However, if you place a camera at the position of the virtual image, it is not possible to record an image. The virtual image is upright and the magnification is positive in this case.

The focal length is positive for a converging lens and is negative for a diverging lens. Diverging lenses always produce virtual upright images.

Magnifying lens
A person cannot focus on an object if it brought too close. The minimum distance that is needed for an eye to focus on an object is called the near point. This distance depends on the person but is typically about 25 cm. If an object is placed just inside the focal length of a converging lens, the diverging rays are bent more parallel by the lens and it is possible to focus on the object even though it is nearer than the near point.

For a magnifying glass, the object is placed closer to the lens than the focal length and the eye sees a larger virtual image. The magnification is approximately $M = \frac{0.25}{f}$ where $f$ is the focal length measured in meters.