Physik M
2.7.2014

Name
Matrikelnr.

Problem 1

Eine Biene befindet sich bei $\vec{r} = 0$ zum Zeitpunkt $t = 0$. Die Geschwindigkeit der Biene ist,

$v_y$

$v_x$

Hierbei ist $t$ die Zeit in Sekunden. Wo ist die Biene zum Zeitpunkt $t=$  s?

$\vec{r}=$ $\hat{x}+ $ $\hat{y}$  [m]

Problem 2

Welche Arbeit wird benötigt, um ein Elektron von der Position

 [m]

zur Position

 [m]

in einem Schwerefeld

 [N] zu bewegen?

$q=$-1.6022 × 10-19 C ist die Ladung des Elektrons, $m_e=$9.11 × 10-31 kg ist die Masse des Elektrons.

$W = $ [J] 

Problem 3

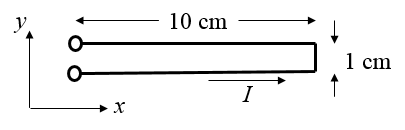
Ein Strom von $I=$  [A] fließt durch eine U-förmiges Drahtsegment. Die Stromrichung ist in der Abbildung dargestellt.

Dieses Drahtsegment befindet sich in einem konstanten magnetischen Feld:

Wie groß ist die Kraft auf das Segment?

$\vec{F} = $ $\hat{x} + $ $\hat{y} + $ $\hat{z}$ [N] 

Problem 4

Ein Gewicht der Masse  kg schwingt an einer Feder mit der linearen Federkonstante $k=$  N/m. Die Schwingungen werden mit dem linearen Dämpfungskoeffizienten $b =$  N s/m gedämpft. Ein Motor zwingt das Gewicht zu schwingen. Treibt der Motor nach dem Einschalten das Gewicht eine derart lange Zeit an, sodaß das Einschwingen vollständig abgeklungen ist, dann kann die Bewegung des Gewichtes so beschrieben werden:

Wie groß ist die auf das Gewicht wirkende Gesamtkraft zur Zeit $t=$  s ?

$F=$  [N] 

Problem 5

Die Position eines mit Überschallgeschwindigkeit fliegenden Flugzeugs sei:

Hierbei ist die Zeit $t$ in Sekunden angegeben.

Die Schockwelle formt einen Kegel um den Geschwindigkeitsvektor. Was ist der Winkel zwischen der Schockwelle und dem Geschwindigkeitsvektor?

$\theta=$  [deg] 

Die Schallgeschwindigkeit ist $c=$ 340 m/s.

Problem 6

Ein Objekt befindet sich im Abstand von  cm vor einer dünnen Linse. Das Bild dieses Objekts erscheint im Abstand von  cm hinter der Linse. Das Bild ist reel und invertiert. Was ist die Brennweite der Linse?

$f=$  [cm]