Problem 1

Ein Schnellkäfer springt, indem er seine Beine schnell austreckt. Dadurch erreicht er eine Beschleunigung von etwa 400$g$. Dies ist deutlich mehr als ein Mensch aushalten könnte.

Ein Schnellkäfer springt gerade in die Höhe. Während der ersten  mm seines Sprungs drückt er mit den Beinen gegen den Boden um so eine konstante Beschleunigung von  m/s² zu erreichen.

Wie hoch springt der Käfer? Vernachlässigen Sie den Luftwiderstand.

Zur Lösung dieses Problems kann entweder die gesamte Trajektorie berechnet, oder mit der Energieerhaltung gearbeitet werden.

Problem 2

Eine Box der Masse  kg wird  Meter über den Boden geschleift, indem an einem Seil mit der Kraft  N gezogen wird. Das Seil wird unter einem Winkel von 45 Grad zur Vertikalen gezogen.

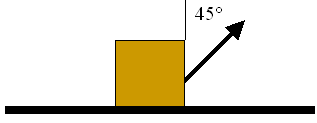
Wenn sich die Box bewegt, wandelt die Reibung mechanische Energie in Wärme um. Wieviel thermische Energie wurde erzeugt nachdem die Box aufgehört hat sich zu bewegen?

Problem 3

Das elektrostatische Potential einer linearen Diode hat die Form

in der Umgebung - μm < $x$ <  μm. $x$ wird hier in Metern gemessen. Da das elektrostatische Potential nur in $x$-Richtung abweicht, hat das elektrische Feld nur eine $x$-Komponente. Wie lautet das elektrische Feld in dieser Umgebung?

Problem 4

Protonen haben eine Masse $m_p=1.6726\times 10^{-27}$ kg und eine Ladung $q=1.6022\times 10^{-19}$ C. Die anfängliche kinetische Energie eines Protons ist Null. Es wird nun durch eine Spannung $V$ in die positive $x$ Richtung beschleunigt. Das Proton erreicht dann eine kreisförmige Umgebung mit einem Radius von  cm, mit einem Magnetfeld  T in $z$ Richtung. Das Proton verlässt die Umgebung in $-y$ Richtung. Das heißt, dass der Radius des Pfades, dem das Proton folgt, ebenfalls  cm beträgt.

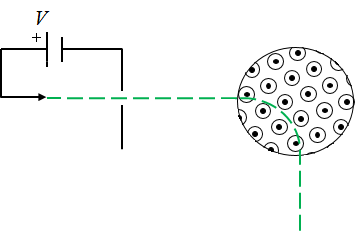
Welche Geschwindigkeit haben die Protonen?

Wie groß ist die Spannung $V$, die benutzt wurde um das Proton zu beschleunigen?

Problem 5

Licht wird an einem Einzelspalt der Weite 50 μm gebeugt und folgendes Beugungsmuster wird auf einem Schirm beobachtet, welcher sich 2 Meter entfernt befindet.

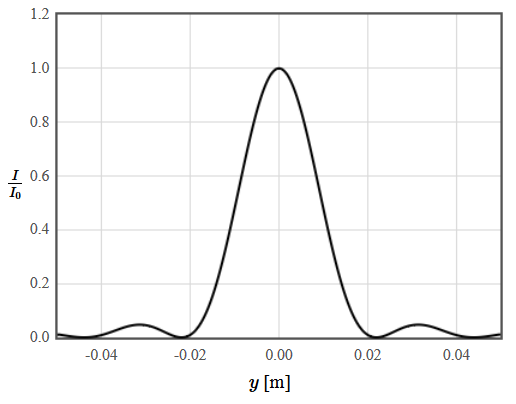
Wie groß ist die Wellenlänge des Lichts, welches in diesem Experiment benutzt wird?

Problem 6

Ein Lichtstrahl, der unter einem Winkel $\phi_1=$ 0.0 rad zur optischen Achse ausgesandt wird, erreicht eine planarkonvexe Linse, 1 cm von der optischen Achse. Die gekrümmte Seite der plankonvexen Linse hat einen Radius 100 cm, die andere Seite ist flach. Der Brechungsindex der Linse ist 2. und der Brechungsindex der Umgebungsluft ist $n=1$.

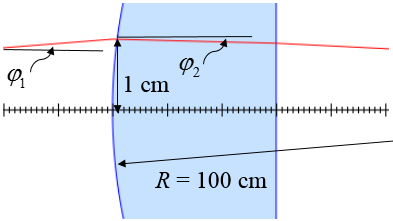
Wie groß ist der Winkel, den der Strahl zur optischen Achse einnimmt, nachdem er die konvexe Grenzfläche passiert hat?