Vorname
Nachname
Matrikelnr.
Problem 1
Ein Teilchen der Masse m = Gramm schwimmt auf der Wasseroberfläche an der Position $\vec{r} = 0$. Nun breitet sich eine zweidimensionale Oberflächenwelle auf der Wasseroberfläche aus. Diese verursacht eine Auslenkung $z$ eines Punktes auf der Oberfläche:
Dabei ist $t$ in Sekunden und Abstände in Metern gemessen. Das Teilchen führt dank der Welle eine Auf- und Abbewegung aus, d.h., in $z$-Richtung normal zur einer glatten Wasseroberfläche.
Wie groß ist die Geschwindigkeit der Wasserwellen?
$v$ = [m/s]
Berechnen Sie die Kraft auf das Teilchen zur Zeit t = Sekunden.
Problem 2
Sei das elektrostatische Potential in einem räumlichen Bereich gegeben durch [V]. Dabei ist $x$ in Metern angegeben. Wie groß ist das elektrische Feld in diesem Bereich?
Protonenmasse: $1.6726231\times 10^{-27}$ kg, Ladung des Protons: $1.60217733\times 10^{-19}$ C.
Problem 3
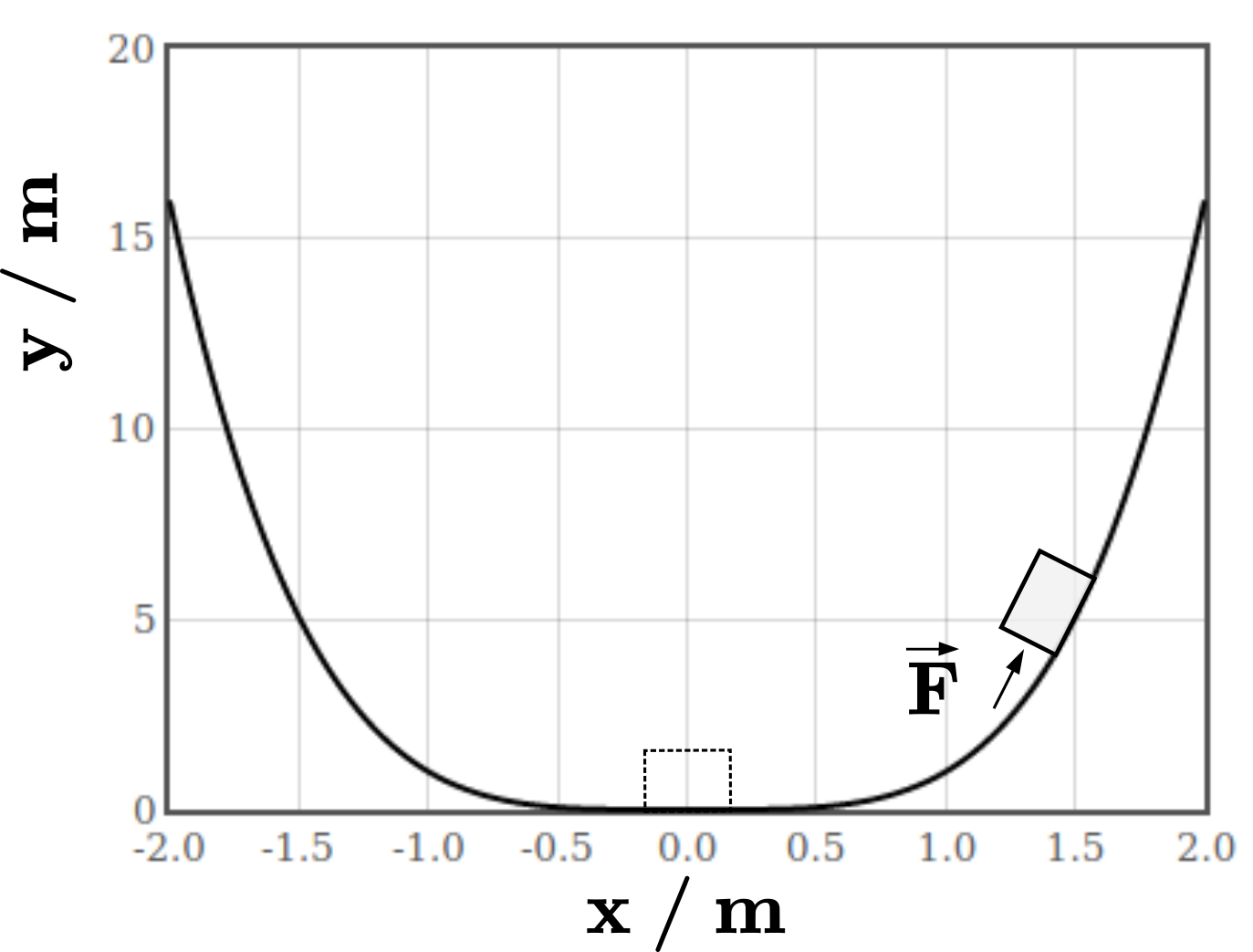
Ein Klotz der Masse g wird auf einer reibungsfreien Oberfläche von $x=0$ nach $x=1.5$ m bewegt. Die Oberfläche hat die Form $y=x^4$, wobei $y$ in Metern gegeben sei. Die Steigung der Oberfläche beträgt $\frac{dy}{dx}=4x^3$ an jedem Punkt.

Welche Kraft wird benötigt, um den Klotz an $x=1.5$ m zu halten?
$\vec{F} =$ $\hat{x}$ + $\hat{y}$ [N]
Wieviel Arbeit muss geleistet werden, um den Klotz von $x=0$ zu $x=1.5$ m zu bewegen?
$W =$ [J]
Der Klotz wird an seiner Ruheposition bei $x=1.5$ m losgelassen und gleitet hinab. Wie schnell bewegt er sich, wenn er $x=0$ erreicht?
$v =$ [m/s]
Die Erdbeschleunigung ist 9.81 m/s².
Problem 4
Ein Elektron befindet sich in zeitunveränderlichen elektrischen und magnetischen Felder,
[V/m],
Zur Zeit $t=0$ befindet sich das Elektron an der Position
[m],
und hat eine konstante Geschwindigkeit von
\[ \begin{equation} \vec{v}= 22000 \hat{x} \,\text{[m/s].} \end{equation} \]Elektronenmasse: $1.6726231\times 10^{-27}$ kg, Elektronladung: $-1.60217733\times 10^{-19}$ C.
Problem 5
Ein Gewicht der Masse g hängt bewegungslos auf ein Feder bei $y=0$ m. Die Federkonstante ist $k=$ N/m.
Bei $t=0$ wurde dem Gewicht ein Schub gegeben: $y(t=0)=0$ m, $v_y(t=0)=-1$ m/s.
Wo ist das Gewicht zum Zeitpunkt $t =$ s? Die Reibung kann vernachlässigt werden.
Problem 6
Lichtstrahlen, die von einem an $o$ befindlichen Objekt emittierten werden, passieren eine Zerstreuungslinse.
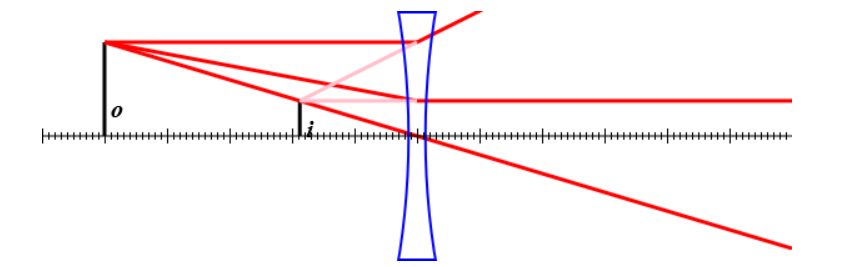
Die kleine Teilung des Maßstabes ist in mm.
Wie lautet die Brennweite der Linse?
$f=$ [cm]
Wie lautet die Vergrößerung der Linse?
$m=$
Das Vorzeichen ist sowohl bei der Brennweite als auch Vergrößerung wichtig!