Problem 1
The velocity vector of a particle of mass $m=$ g is,

Here $t$ is the time in seconds.

What is the force that acts on this particle at time $t=1$ s?

$\vec{F} = $ $\hat{x} + $ $\hat{y} + $ $\hat{z}$ [N] 

Problem 2
Two long straight parallel wires are  cm apart. The current in the first wire is  mA and the current in the second wire is  mA. What is the magnetic field at the second wire due to the current in the first wire?

$B=$ [T]

What is the force per unit length between the wires?

$F=$ [N/m]

Problem 3

The electrostatic potential in a region of space is,

Here $x$ is the position measured in meters.

What is the electric field in this region? The electric field is a function of $x$.

$\vec{E} = $ $\hat{x} + $ $\hat{y} + $ $\hat{z}$ [V/m] 

What is the charge density in this region? The charge density is a function of $x$.

$\frac{\rho}{\epsilon_0}$ = [C/m³]

How much energy is required to move an electron from $\vec{r}=0$ to $\vec{r}=2\hat{x} + 2\hat{y}+ 2\hat{z}$ m?

$E$ = [J]

Electron charge: $-1.6022\times 10^{-19}$ C, Electron mass: $9.1093897\times 10^{-31}$ kg, $\epsilon_0=8.854187817\times 10^{-12}$ F m^-1.

Problem 4

Two dimensional waves are sent out by two point sources located at $\vec{r}_1=2\hat{x}$ [m] and $\vec{r}_2=2\hat{y}$ [m]. Both of these sources radiate with the same frequency and the peaks of the waves leave the sources at the same time. The wavelength is  m.

Give a point where constructive interference occurs.

$\vec{r}_{\text{constructive}}=$ $\hat{x} +$ $\hat{y}$ [m]

Problem 5

The position vector of an airplane traveling at supersonic speed is,

Here $t$ is measured in seconds.

The shock wave forms a cone around the velocity vector. What is the angle between the shock wave and the velocity vector?

$\theta=$  [deg]

When is the sonic boom heard at $\vec{r} = 0$?

$t=$  [s]

The speed of sound is $c=$ 340 m/s.

Problem 6

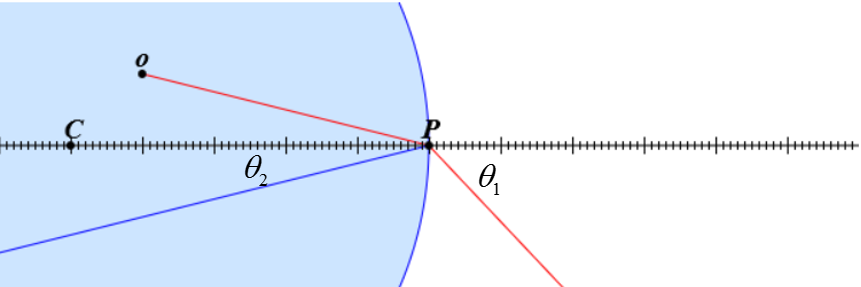
A light ray emitted from point $o$ ($x=-4$ cm, $y=1$ cm) strikes a spherical interface at point $P$ ($x=0$ cm, $y=0$ cm). The radius of the curved interface is 5 cm. The index of refraction is $n_1=3$ left of the interface and $n_2=1$ to the right of the interface.

What is the angle $\theta_1$?

$\theta_1 =$ [rad]

What is the angle $\theta_2$?

$\theta_2 =$ [rad]