Problem 1
Die Bahnkurve eines Teilchens der Masse $m=$  g ist,

Dabei ist $t$ die Zeit in Sekunden.

Welche Kraft wirkt auf das Teilchen zur Zeit $t=$  s?

$\vec{F} = $ $\hat{x} + $ $\hat{y} + $ $\hat{z}$ [N] 

Problem 2

Ein langer, gerader Draht liegt entlang der $y$-Achse eines Koordinatensystems. Durch diesen Draht fließt ein elektrischer Strom  mA in die positive $y$-Richtung. Ein Elektron fliegt über den Draht. Das Elektron hat die Geschwindigkeit

$\vec{v}=$$\hat{x} -$$\hat{y}$ [m/s].

als es an der Position

$\vec{r}= 0\hat{x}+0\hat{y}+0.01\hat{z}$ [m]

ist.

Wie groß ist die Lorentzkraft des magnetischen Feldes auf das Elektron?

$\vec{F}=$ $\hat{x} +$ $\hat{y} +$ $\hat{z}$ [N]

Elektronmassa = $9.10938356 \times 10^{-31}$ kg  Elektronladung = $-1.6021766208 \times 10^{-19}$ C

Problem 3

Eine Kugel mit der Masse  kg ist an einer nicht linearen Feder angebracht. Die Federkraft ist $F_{\text{feder}}=-$$x|x|$ N. $x$ ist hierbei die Auslenkung der Feder in Metern. Die Feder wird 2 cm von ihrer Ruheposition ausgelenkt.

(a) Wie viel Energie wird benötigt, um die Feder von $x=0$ bis $x=2$  cm zu dehnen?

Die Masse wird von $x=2$ cm aus dem Ruhezustand losgelassen. Wenn die Feder versucht sich wieder in ihre Ruheposition zurück zu bewegen wirkt auf die Masse eine Reibungskraft, die der Bewegungsrichtung entgegensetzt ist: $F_{\text{drag}}=-$$v_x^3$ N.

Welche Differentialgleichung muss gelöst werden, um die Bewegung der Kugel bestimmen zu können?

Wo ist der Ball zur Zeit $t=3$ s?

Problem 4
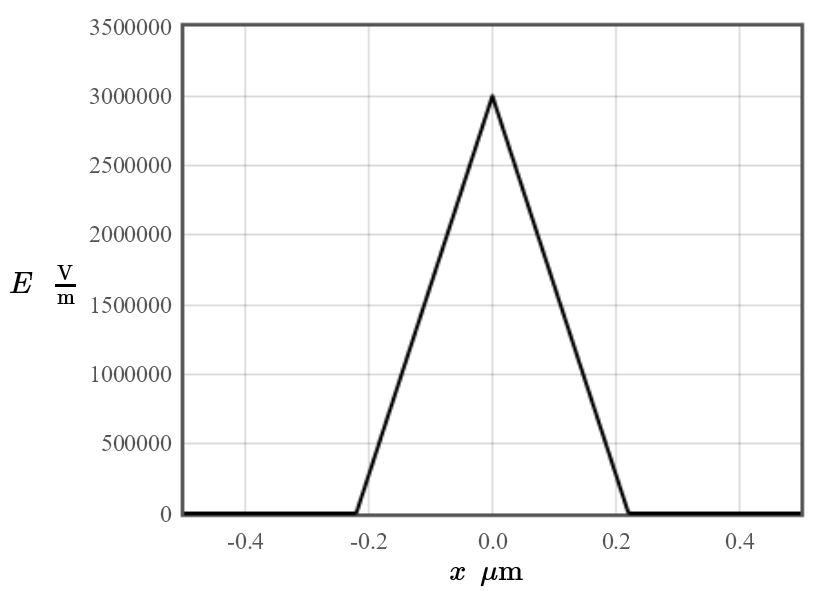
Ein elektrisches Feld in einer Solarzelle zeigt normal auf die Oberfläche der Solarzelle. Das elektrische Feld ist in der folgenden Grafik abgebildet.

Zeichnen Sie die Ladungsdichte, welche zu dem elektrischen Feld gehört. Kennzeichnen Sie die Maximal- und Minimalwerte der Ladungsdichte.

Zeichnen Sie das zu dem elektrischen Feld gehörende elektrostatische Potential. Kennzeichnen Sie die Maximal- und Minimalwerte des elektrostatischen Potentials.

Die relative dielektrische Konstante von Silizium ist $\epsilon_r=12$. Die elektrische Feldkonstante ist $\epsilon_0=8.85\times 10^{-12}$ F/m.

Problem 5

Zweidimensionale Wellen werden von zwei punktförmigen Quellen, die sich an $\vec{r}_1=-2\hat{x}$ [m] und $\vec{r}_2=2\hat{x}$ [m] befinden ausgesendet. Das resultierende Interferenzmuster wird beschrieben durch,

Hier werden $z$ und $r$ in Metern und $t$ in Sekunden angegeben.

Wie groß ist die Wellenlänge der Wellen?

$\lambda=$ [m]

Wie lautet die Winkelfrequenz der Wellen?

$\omega=$ [rad/s]

Wie lautet die Wellengeschwindigkeit?

$v=$ [m/s]

Wie lautet die Amplitude der Schwingung $|\mathcal{A}|$ an der Stelle $\vec{r}=2\,\hat{y}$ m?

$|\mathcal{A}|=$ [m]

Problem 6
Eine konvexe Grenzfläche hat einen Radius von $R=$ 5 cm. Ein an der Position $o$ $(x_0=$ -3 cm, $y_0=$ 1 cm$)$ emittierter Lichtstrahl trifft auf diese Fläche am Punkt $P$ $(x_P=$  cm, $y_0=$  cm$)$. Der Brechungsindex ist $n_1=1$ links und $n_2=$ 1. rechts der Grenzfläche.

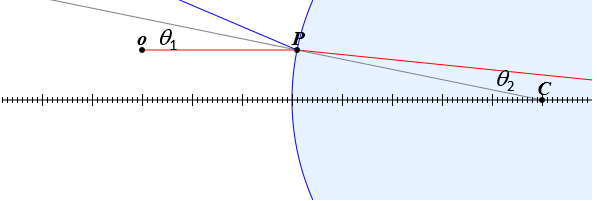
(a) Wie groß ist der Winkel θ₂?

(b) Auf der linken Seite der Grenzfläche ist die Frequenz und Wellenlänge des Lichtstrahls $f=5\times 10^{14}$ Hz and $\lambda=600$ nm. Wie groß sind Frequenz und Wellenlänge auf der rechten Seite?