Name
Matrikelnr.
Problem 1
Ein Elektron ($m=9.11\times10^{-31}$ kg, $q=-1.6022\times10^{-19}$ C) befindet sich in einem elektrischen Feld,
Zur Zeit $t=0$ befindet sich das Elektron bei $\vec{r}=0$ und hat eine Geschwindigkeit von Null ($\vec{v}=0$). Wie lautet die Geschwindigkeit des Elektrons zur Zeit $t=1$ μs?
Problem 2
Ein Ball der Masse Gramm ist mit einer nichtlinearen Feder verbunden. Die Feder übt eine Kraft [N] aus, mit $x$ der Ausdehnung der Feder in Metern. Der ball schwingt horizontal auf einem Tisch. Vernachlässigen Sie Reibungskräfte. Die Feder wird um cm komprimiert, dann wird das Gewicht losgelassen.
Wie groß ist die maximale Geschwindigkeit der Masse?
Problem 3
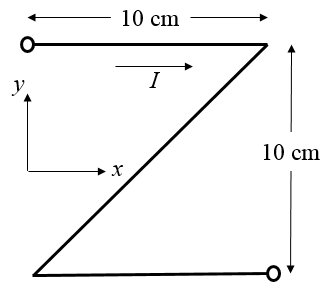
Ein Strom von $I=$ [A] fließt durch eine Z-förmiges Drahtsegment. Das Drahtsegment liegt in der Ebene $z = 0$. Die Stromrichung ist in der Abbildung dargestellt.

Dieses Drahtsegment befindet sich in einem konstanten magnetischen Feld: