First Name
Last Name
Student Number.
Problem 1
An electron (Charge $q=-1.6022\times10^{-19}\,\text{C}$, Mass $m=9.1093897\times 10^{-31}\,\text{kg}$) moves it an electric field. The position vector of the electron is,
Here $t$ is in seconds. What is the electric field?
$\vec{E} = $ $\hat{x} + $ $\hat{y} + $ $\hat{z}$ [V/m]
Problem 2
A weight with a mass of 100 g hangs motionless from a spring at $y=0$ m. The spring constant is $k=$ N/m.
At $t=0$, the weight is pushed so that its velocity is: $y(t=0)=0$ m, $v_y(t=0)=-1$ m/s.
There is a frictional force that acts in the direction opposite to the velocity, $\vec{F}_{fric}= -0.1\left|\frac{d\vec{y}}{dt}\right|\frac{d\vec{y}}{dt}$.
Where is the weight at time $t =$ s?
This problem must be solved numerically.
Problem 3
A box with a mass kg is dragged meters across the floor by pulling on a rope with a force $\vec{F} = 3\,\hat{x}+5\,\hat{y}+7\,\hat{z}$ N.
How much work is required to move the box?
Problem 4
An electric field is described by:
$$\vec{E}= 10^4\exp \left(-\frac{x}{10^{-6}}\right)\,\hat{x}\quad\text{V/m}$$What is the difference in the electrostatic potential between points $x = 0$ m and $x= 0.001$ m?
$\phi(x = 0.001) - \phi(x = 0) = $ [V]
Problem 5
Two-dimenional waves are radiated by two sources at $\vec{r}_1=-3\hat{x}$ [m] and $\vec{r}_2=3\hat{x}$ [m]. The resulting interference pattern is described by,
Here $z$ and $r$ are measured in meters and $t$ in seconds.
What is the wavelength of the waves?
$\lambda=$ [m]
What is the angular frequency of the waves?
$\omega=$ [rad/s]
What is the wave velocity?
$v=$ [m/s]
What is the amplitude of the interference pattern at $t=3$ s at the point $\vec{r}=0$?
$z=$ [m]
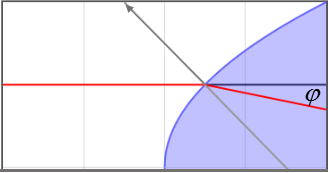
Problem 6
A light ray (red) strikes a parabolic interface. The vector normal to the interface at this point (gray) is $-\hat{x}+\hat{y}$. The index of refraction is $n_1=1$ left of the interface and $n_2=$ 2. to the right of the interface. What is the angle $\varphi$ of the refracted beam to the horizontal?