Vorname
Nachname
Matrikelnr.
Problem 1
Ein Elektron (Ladung $q=-1.6022\times10^{-19}\,\text{C}$, Masse $m=9.1093897\times 10^{-31}\,\text{kg}$) bewegt sich in einem elektrischen Feld. Der Ortsvektor des Elektrons ist
Dabei ist $t$ die Zeit in Sekunden. Wie lautet das elektrische Feld?
$\vec{E} = $ $\hat{x} + $ $\hat{y} + $ $\hat{z}$ [V/m]
Problem 2
Ein Gewicht der Masse 100 g hängt bewegungslos auf ein Feder bei $y=0$ m. Die Federkonstante ist $k=$ N/m.
Bei $t=0$ wurde dem Gewicht ein Schub gegeben: $y(t=0)=0$ m, $v_y(t=0)=-1$ m/s.
Es wirkt eine Reibungskraft, die entgegen der Richtung der Geschwindigkeit des Gewichts zeigt, $\vec{F}_{fric}= -0.1\left|\frac{d\vec{y}}{dt}\right|\frac{d\vec{y}}{dt}$ N.
Wo ist das Gewicht zum Zeitpunkt $t =$ s?
Dieses Problem muss numerisch gelöst werden.
Problem 3
Eine Box der Masse kg wird Meter über den Boden geschleift, indem an einem Seil mit der Kraft $\vec{F} = 3\,\hat{x}+5\,\hat{y}+7\,\hat{z}$ N gezogen wird.
Welche Arbeit muss aufgewandt werden, um die Box zu bewegen?
Problem 4
Das elektrische Feld sei beschrieben durch:
$$\vec{E}= 10^4\exp \left(-\frac{x}{10^{-6}}\right)\,\hat{x}\quad\text{V/m}$$Wie gross ist die Änderung des elektrostatischen Potentials zwischen $x = 0$ m und $x= 0.001$ m?
$\phi(x = 0.001) - \phi(x = 0) = $ [V]
Problem 5
Zweidimensionale Wellen werden von zwei punktförmigen Quellen, die sich an $\vec{r}_1=-3\hat{x}$ [m] und $\vec{r}_2=3\hat{x}$ [m] befinden ausgesendet. Das resultierende Interferenzmuster wird beschrieben durch,
Hier werden $z$ und $r$ in Metern und $t$ in Sekunden angegeben.
Wie groß ist die Wellenlänge der Wellen?
$\lambda=$ [m]
Wie lautet die Winkelfrequenz der Wellen?
$\omega=$ [rad/s]
Wie lautet die Wellengeschwindigkeit?
$v=$ [m/s]
Was ist die Amplitude zum Zeitpunkt $t=3$ s an der Stelle $\vec{r}=0$?
$z=$ [cm]
Problem 6
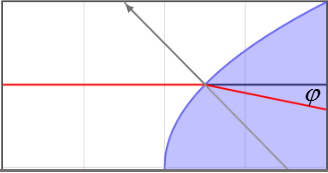
Ein Lichtstrahl (rot) trifft auf eine parabolische Grenzfläche. Der Normalvektor auf der Grenzfläche (grau) sei $-\hat{x}+\hat{y}$. Der Brechungsindex ist $n_1=1$ links und $n_2=$ 2. rechts der Grenzfläche. In welchem Winkel $\varphi$ zur Horizontalen wird der Lichtstrahl gebrochen?