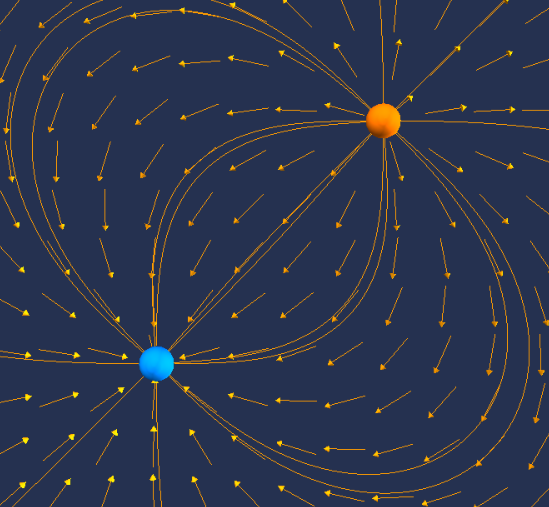
Two point charges

If there is more than one point charge, the expressions for the electric fields and the electrostatic potentials can be added together for the different charges. For two charges, the electric field is,

$$\vec{E}(\vec{r})= \frac{q_1}{4\pi \epsilon_0}\frac{\vec{r}-\vec{r}_1}{ |\vec{r}-\vec{r}_1|^3} + \frac{q_2}{4\pi \epsilon_0}\frac{\vec{r}-\vec{r}_2} {|\vec{r}-\vec{r}_2|^3}\hspace{1cm}\text{[V/m]},$$

and an electrostatic potential is,

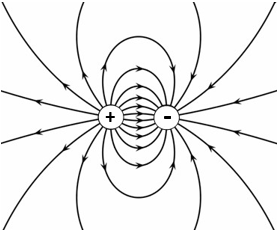
$$\varphi(\vec{r})= \frac{q_1}{4\pi \epsilon_0 |\vec{r}-\vec{r}_1|}+\frac{q_2}{4\pi \epsilon_0 |\vec{r}-\vec{r}_2|}\hspace{1cm}\text{[V]}.$$

Below the electric field pattern formed by two equal but opposite charges is shown. The electric field lines point from the positive charge to the negative charge.

The charges can be moved around interactively in this Electric field of two point charges simulation from MIT.

The Coulomb force and the electric field are vectors and to calculate the three components of the vector, the following identity is often used,

$$\hat{r}_{2\rightarrow 1} = \frac{\vec{r}_1-\vec{r}_2}{|\vec{r}_1-\vec{r}_2|}= \frac{x_1-x_2}{|\vec{r}_1-\vec{r}_2|}\hat{x}+ \frac{y_1-y_2}{|\vec{r}_1-\vec{r}_2|}\hat{y}+ \frac{z_1-z_2}{|\vec{r}_1-\vec{r}_2|}\hat{z}.$$

The force exerted on point charge $q_1$ because of the Coulomb interaction with charge $q_2$ is,

$$\vec{F}= \frac{q_1q_2}{4\pi \epsilon_0 |\vec{r}_1-\vec{r}_2|^2}\hat{r}_{2\rightarrow 1} \quad\text{N}.$$

The force exerted on charge $q_2$ is $-\vec{F}$. The vector $\vec{r}_1-\vec{r}_2$ points from $q_2$ to $q_1$. If $q_2$ and $q_1$ have the same sign, the force pushes the two charges apart and if $q_2$ and $q_1$ have opposite signs, the force pulls the two charges together.

The components of the force vector are,

$$F_x = \frac{q_1q_2(x_1-x_2)}{4\pi \epsilon_0 |\vec{r}_1-\vec{r}_2|^3}\,\,\text{N},\qquad F_y = \frac{q_1q_2(y_1-y_2)}{4\pi \epsilon_0 |\vec{r}_1-\vec{r}_2|^3}\,\,\text{N},\qquad F_z = \frac{q_1q_2(z_1-z_2)}{4\pi \epsilon_0 |\vec{r}_1-\vec{r}_2|^3}\,\,\text{N}.$$

Question