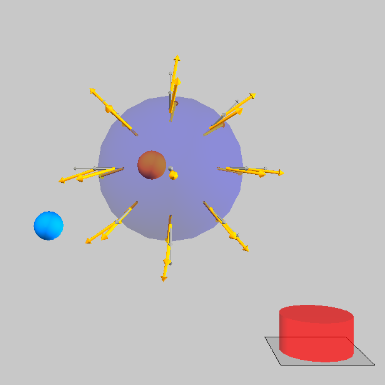
Divergence

Since an electric field is associated with every point charge, you can tell what the total charge in some volume is by looking at the electric field lines coming out of that volume. If more electric field lines point out than point in, the charge in the volume is positive and if more electric field lines point in than point out, the charge in the volume is negative. This can be stated mathematically with the divergence. The divergence of the electric field is,

$$\nabla \cdot \vec{E} = \left( \frac{\partial }{\partial x}\hat{x} +\frac{\partial }{\partial y}\hat{y} +\frac{\partial }{\partial z}\hat{z}\right)\cdot \vec{E}=\frac{\partial E_x}{\partial x} +\frac{\partial E_y}{\partial y} +\frac{\partial E_z}{\partial z}.$$

$\vec{E}(x,y,z)=$  $\hat{x}$ +  $\hat{y}$ +  $\hat{z}$  
$\nabla\cdot \vec{E} = $ () + () + ()

If $\frac{\partial E_x}{\partial x} > 0$, more of the $x$-component of the electric field lines is pointing out of the volume than pointing in.

The precise relationship between the divergence of the electric field and the charge is given by Gauss's law,

$$\nabla \cdot \vec{E} = \frac{\rho}{\epsilon_0}.$$

Here $\rho$ is the charge density and $\epsilon_0 = 8.854187817 \times 10^{-12}$ F/m is the permitivity constant. Gauss's law can also be expressed in integral form,

$$\int_S\vec{E}\cdot d\vec{s} =\frac{q}{\epsilon_0}.$$

Here $S$ is a closed surface made up of many surface elements $d\vec{s}$ which has a magnitude equal to the area of the surface element and a direction normal to the surface $q$ is the total charge enclosed inside the surface.


Gauss's law

Question