Electric deflection of an electron beam

Electrons are accelerated through a voltage $V_x$ towards a positively charged plate. Some of the electrons pass through a small hole in the plate and form and electron beam that travels to a region where an electric field is established by applying a voltage $V_y$ between two metal plates spaced a distance $d$ apart.

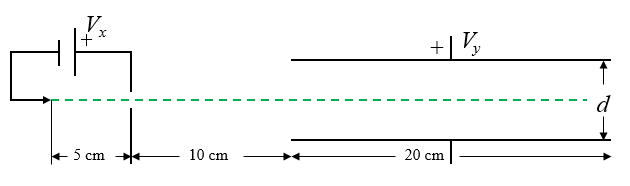
The electrons are accelerated from rest to the positively charged plate in a distance of 5 cm. The electrons get deflected as they pass through the electric field between the plates. In the plot below, the vertical axis has been expanded to show the deflection more clearly.

$\vec{F}=m\frac{d^2\vec{r}}{dt^2} = qE_xH(0.05-x)\,\hat{x} +qE_yH(0.1-|x-0.25|)\,\hat{y}$

 

  

$V_x=$ 5000 [V]

$V_y=$ 1 [V]

$d=$ 0.05 [m]

$E_x=\frac{V_x}{0.05}=$  [V/m]
$E_y=\frac{V_y}{d}=$  [V/m]

 3-D motion differential equation solver 

$ F_x=$

 [N]

$ F_y=$

 [N]

$ F_z=$

 [N]

$ m=$

 [kg]
Initial conditions: 

$t_0=$

 [s] 

$\Delta t=$

 [s]

$x(t_0)=$

 [m] 

$N_{steps}$

$v_x(t_0)=$

 [m/s] 

Plot:

vs.

$y(t_0)=$

 [m] 

$v_y(t_0)=$

 [m/s] 

$z(t_0)=$

 [m] 

$v_z(t_0)=$

 [m/s] 


 $t$ [s] $x$ [m] $y$ [m] $z$ [m] $v_x$ [m/s] $v_y$ [m/s] $v_z$ [m/s] $F_x$ [N] $F_y$ [N] $F_z$ [N] $P$ [W] $E_{\text{kin}}$ [J] $W$ [J]