Electric field produced by a uniformly-charged long straight wire
Consider a uniformly charged very long rod aligned with the $z$-axis. The charge density is $\lambda$ Coulombs/meter. If the rod is cut into many sections each $dz$ long, then the charge in each section is $\lambda dz$.
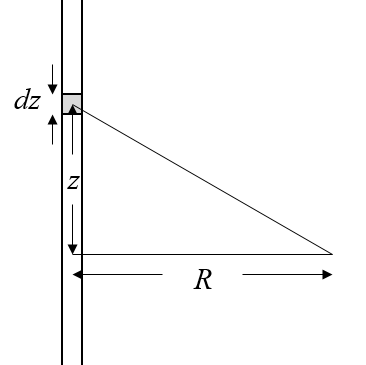
This small charge will contribute a small electric field $d\vec{E}$ to the electric field at a radial distance $R$ from the rod,
$$d\vec{E} = \frac{\lambda dz}{4\pi\epsilon_0(R^2+z^2)}\frac{R}{\sqrt{R^2+z^2}}\hat{R} - \frac{\lambda dz}{4\pi\epsilon_0(R^2+z^2)}\frac{z}{\sqrt{R^2+z^2}}\hat{z}.$$This electric field has a magnitude, $|d\vec{E}| =\frac{|\lambda |dz}{4\pi\epsilon_0r^2}$, where $r^2 = R^2+z^2$ and a direction given by,
$$d\hat{E} = \frac{R}{\sqrt{R^2+z^2}}\hat{R} - \frac{z}{\sqrt{R^2+z^2}}\hat{z}.$$The total electric field at radial distance $R$ will be the sum of all of the charge contributions from each section $dz$. This can be written as two integrals,
$$\vec{E} = \int\limits_{-\infty}^{\infty}\frac{\lambda dz}{4\pi\epsilon_0(R^2+z^2)}\frac{R}{\sqrt{R^2+z^2}}\hat{R}- \int\limits_{-\infty}^{\infty}\frac{\lambda dz}{4\pi\epsilon_0(R^2+z^2)}\frac{z}{\sqrt{R^2+z^2}}\hat{z}.$$The second integral is an odd function evaluated over an even interval so it is zero. It is also clear from symmetry that an infinitely long rod should not produce an electric field with a component parallel to the rod. The remaining integral can be performed using the identity,
$$\int\limits_{-\infty}^{\infty}\frac{dz}{\left(R^2+z^2\right)^{3/2}} = \frac{2}{R^2}.$$The electric field around a long straight uniformly-charged rod is directed in the radial direction $\hat{R}$,
|
$\hspace{0.5cm}\large \vec{E} = \frac{\lambda}{2\pi\epsilon_0 |\vec{R}|}\hat{R}\quad\text{V/m}.\hspace{0.5cm}$ |
The electrostatic potential is,
$$\varphi (\vec{r})= \frac{-\lambda}{2\pi \epsilon_0 }\ln\left(|\vec{R}|\right)\quad\text{[V]}.$$This can be checked by taking the gradient of the electrostatic potential $\vec{E}=-\nabla \varphi$.
Arbitrary orientation of the line
Consider a collection of uniformly charged long rods. The position of rod $i$ is specified by giving a direction $\hat{n}_i$ that passes through the point $\vec{r}_{i0}$. The vector pointing from $\vec{r}_{i0}$ to some other point $\vec{r}$ is $\vec{r}-\vec{r}_{i0}$. This vector can be decomposed into a distance along the rod and a distance perpendicular to the rod, $\vec{r}-\vec{r}_{i0} = \vec{d}_{\parallel} + \vec{d}_{\perp}$, where the parallel component is the projection of $\vec{r}-\vec{r}_{i0}$ onto $\hat{n}_i$, $\vec{d}_{\parallel}=\hat{n}_i\cdot(\vec{r}-\vec{r}_{i0})\,\hat{n}_i$. The shortest distance from the rod to point $\vec{r}$ is $\vec{R}_i = \vec{d}_{\perp}=(\vec{r}-\vec{r}_{i0})-\vec{d}_{\parallel}$.
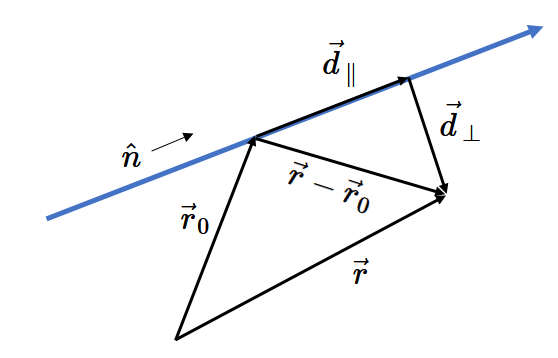
The electrostatic potential and electric field at point $\vec{r}$ due to a collection of charged rods is,
$$\varphi (\vec{r})= \sum_{i=1}^{N}\frac{-\lambda_i}{2\pi \epsilon_0 }\ln\left(|\vec{R}_i|\right)\quad\text{[V]},$$ $$\vec{E}(\vec{r}) = \sum_{i=1}^{N}\frac{\lambda_i}{2\pi\epsilon_0 |\vec{R}_i|}\hat{R}_i\quad\text{V/m}.$$where $\vec{R}_i = (\vec{r}-\vec{r}_{i0})-\hat{n}_i\cdot(\vec{r}-\vec{r}_{i0})\,\hat{n}_i$.