Electric field produced by a uniform sheet of charge
Consider a uniform sheet of charge at $x=0$. The $y-z$ plane contains charge with a density $\sigma$ Coulombs/m². A point charge at position $(0,y,z)$ has a charge $\sigma dydz$.
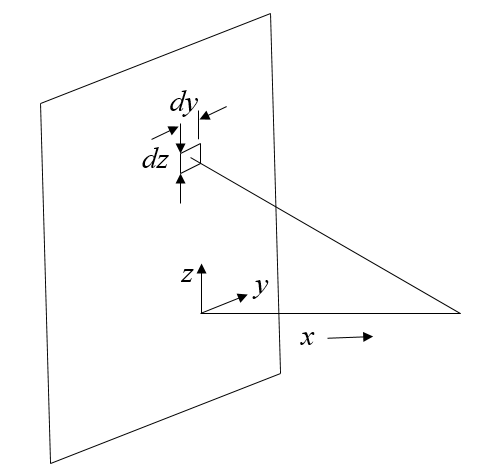
This small charge will contribute a small electric field $d\vec{E}$ to the electric field at position $x$,
$$d\vec{E} = \frac{\sigma dydz}{4\pi\epsilon_0(x^2+y^2+z^2)}\frac{x}{\sqrt{x^2+y^2+z^2}}\hat{x} - \frac{\sigma dydz}{4\pi\epsilon_0(x^2+y^2+z^2)}\frac{y}{\sqrt{x^2+y^2+z^2}}\hat{y}-\frac{\sigma dydz}{4\pi\epsilon_0(x^2+y^2+z^2)}\frac{z}{\sqrt{x^2+y^2+z^2}}\hat{z}.$$This electric field has a magnitude, $|d\vec{E}| =\frac{|\sigma |dydz}{4\pi\epsilon_0r^2}$, where $r^2 = x^2+y^2+z^2$ and a direction given by,
$$d\hat{E} = \frac{x}{\sqrt{x^2+y^2+z^2}}\hat{x} - \frac{y}{\sqrt{x^2+y^2+z^2}}\hat{y} -\frac{z}{\sqrt{x^2+y^2+z^2}}\hat{z}.$$The total electric field is the sum of all of the charge contributions from each section $dydz$. This is,
$$\vec{E} = \int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}\frac{\sigma dydz}{4\pi\epsilon_0(x^2+y^2+z^2)}\frac{x}{\sqrt{x^2+y^2+z^2}}\hat{x} - \int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}\frac{\sigma dydz}{4\pi\epsilon_0(x^2+y^2+z^2)}\frac{y}{\sqrt{x^2+y^2+z^2}}\hat{y}-\int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}\frac{\sigma dydz}{4\pi\epsilon_0(x^2+y^2+z^2)}\frac{z}{\sqrt{x^2+y^2+z^2}}\hat{z}.$$The second integral vanishes when the integration over $y$ is performed because it is an odd function evaluated over an even interval. Similarly, the third integral vanishes when the integration over $z$ is performed. The electric field only has a component normal to the plane of charge.
$$\vec{E} = \int\limits_{-\infty}^{\infty}\int\limits_{-\infty}^{\infty}\frac{\sigma dydz}{4\pi\epsilon_0(x^2+y^2+z^2)}\frac{x}{\sqrt{x^2+y^2+z^2}}\hat{x}.$$Using the identity,
$$\int\limits_{-\infty}^{\infty}\frac{dz}{\left(R^2+z^2\right)^{3/2}} = \frac{2}{R^2},$$where $R^2 = x^2 + y^2$ yields,
$$\vec{E} = \int\limits_{-\infty}^{\infty}\frac{x\sigma dy}{2\pi\epsilon_0(x^2+y^2)}\hat{x}.$$Using the identity,
$$\int\limits_{-\infty}^{\infty}\frac{dy}{\left(x^2+y^2\right)} = \frac{\pi}{|x|},$$The electric field is,
|
$\hspace{0.5cm} \vec{E} = \frac{\sigma}{2\epsilon_0}\text{sgn}(x)\hat{x}.\quad\text{V/m}.\hspace{0.5cm}$ |
Here $\text{sgn}(x) =1$ for $x > 0$ and $\text{sgn}(x) =-1$ for $x < 0$. If the sheet charge is positive $(\sigma > 0)$, the electric field points away from the sheet charge in the direction normal to the plane on both sides. If the sheet charge is negative $(\sigma < 0)$, the electric field points towards the sheet charge in the direction normal to the plane on both sides.
The electric field produced by a sheet of charge with an arbitrary orientation is,
$$\vec{E}(\vec{r}) = \frac{\sigma}{2\epsilon_0}\text{sgn}((\vec{r}-\vec{r}_0)\cdot\hat{n})\hat{n}.\quad\text{V/m},$$where $\sigma$ is the charge density, $\hat{n}$ is the normal to the plane, $\vec{r}_0$ is a point on the plane, and $\vec{r}$ is the point where the electric field is observed. For an infinite sheet, the electric field is perpendicular to the plane that the charge lies in and has a constant magnitude no matter how far from the plane your are.
The corresponding electrostatic potential is,
$$\phi(\vec{r}) = \frac{-\sigma(\vec{r}-\vec{r}_0)\cdot\hat{n}}{2\epsilon_0}\text{ [V]}.$$