The force on a current carrying wire
When current flows through a wire, the charges are moving. If they move in a magnetic field, they will experience a Lorentz force. Consider a short section of the wire $d\vec{l}$ where the vector points in the direction that the current is flowing.
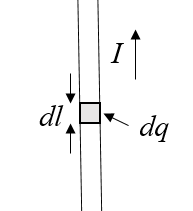
The charge in this section of wire is $dq$ and the Lorentz force on this section of wire is,
$$ d\vec{F}=dq\vec{v}\times \vec{B},$$where $\vec{v}$ is the velocity that the charge is moving. The velocity is $\vec{v} = \frac{d\vec{l}}{dt}$and the current is $I=\frac{dq}{dt}$ so the force on this section of wire can be written as,
$$ d\vec{F}=Id\vec{l}\times \vec{B}.$$If the wire is straight in a constant magnetic field and has a total length $L$ then the force on each segment is the same and the total force is,
$$ \vec{F}=I\vec{L}\times \vec{B},$$Where $\vec{L}$ points in the direction that the current is flowing.
Consider two parallel wires carrying currents $I_1$ and $I_2$ in the $z$-direction.
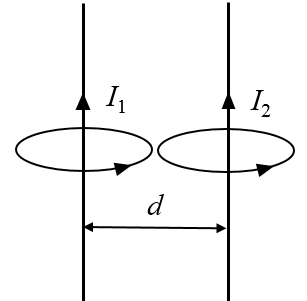
If the wires are separated by a distance $d$, then the magnetic field at wire 1 will be $\vec{B}_1= -\frac{\mu_0I_2}{2\pi d}\hat{y}$ and the magnetic field at wire 2 will be $\vec{B}_2= \frac{\mu_0I_1}{2\pi d}\hat{y}$. The forces per meter on the wires are,
$$\frac{\vec{F}_1}{\text{meter}} = \frac{\mu_0I_1I_2}{2\pi d}\hat{x}\quad\text{N/m}\hspace{1.5cm}\frac{\vec{F}_2}{\text{meter}} = -\frac{\mu_0I_1I_2}{2\pi d}\hat{x}\quad\text{N/m}.$$If the two currents are flowing in the same direction, the wires are pulled towards each other. If the currents are flowing in opposite directions, the wires are pushed apart. The force between two current carrying wires is used to build electric motors.