The magnetic field around an infinitely-long straight wire
A current $I$ [A] flows in the positive $z$-direction through an infinitely long straight wire that lies on the $z$-axis. To calculate the magnetic field, the Biot-Savart law is used. Each wire segment $dz$ contributes a magnetic field at position $\vec{r}$ of,
$$ d\vec{B}(\vec{r})=\frac{\mu_0}{4\pi}\frac{I d\vec{r}_{wire} \times (\vec{r}-\vec{r}_{wire})}{|\vec{r}-\vec{r}_{wire}|^3}\hspace{1cm}\text{[T]}.$$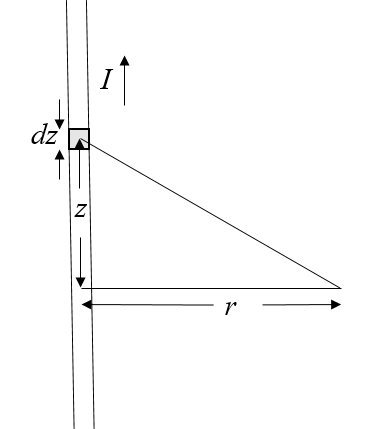
For $\vec{r}$ in the $x-y$ plane $\left(\vec{r}=x\hat{x}+y\hat{y}\right)$, the sum of the contributions from all of the wire segments is,
$$\vec{B}(\vec{r}) = \frac{\mu_0I}{4\pi}\int\limits_{-\infty}^{\infty}\frac{ dz\hat{z} \times \left(x\hat{x}+y\hat{y}-z\hat{z}\right)}{\sqrt{r^2+z^2}^3}\hspace{1cm}\text{[T]}.$$The cross products are $\hat{z}\times\hat{x}=\hat{y}$, $\hat{z}\times\hat{y}=-\hat{x}$, $\hat{z}\times\hat{z}=0$,
$$\vec{B}(\vec{r}) = \frac{\mu_0I}{4\pi}\int\limits_{-\infty}^{\infty}\frac{ xdz \hat{y}}{\sqrt{r^2+z^2}^3}-\frac{\mu_0I}{4\pi}\int\limits_{-\infty}^{\infty}\frac{ ydz \hat{x}}{\sqrt{r^2+z^2}^3}\hspace{1cm}\text{[T]}.$$Using the identity,
$$\int\limits_{-\infty}^{\infty}\frac{dz}{\left(r^2+z^2\right)^{3/2}} = \frac{2}{r^2},$$this can be written,
$$\vec{B}(\vec{r}) = \frac{\mu_0I}{2\pi}\left(\frac{-y}{r^2}\hat{x}+ \frac{x}{r^2}\hat{y}\right)=\frac{\mu_0I}{2\pi r}\hat{z}\times\hat{r}\hspace{1cm}\text{[T]}.$$The magnetic field points in the azimuthal direction perpendicular to both $\hat{z}$ and $\hat{r}$. The magnetic field lines form circles around the wire. The direction of the magnetic field lines is given by teh right hand rule, point the thumb of your right hand in the direction of the current flow and your bent fingers point in the direction of the magnetic field.
| \[ \begin{equation} \hspace{0.5cm}\bbox[10px, border: 1px solid black]{|\vec{B}(\vec{r})|=\frac{\mu_0I}{2\pi r}\hspace{0.5cm}\text{[T]}}\hspace{0.5cm} \end{equation} \] |  |
Ampère's law can be also be used to calculate the magnetic field in this case. The integral form of Ampère's law is,
$$\oint\limits_{C}\vec{B}\cdot d\vec{l}=\mu_0 I_{enc},$$where the magnetic field is integrated along a closed curve $C$ and $I_{enc}$ is the current passing through $C$. For a long straight wire we choose to integrate the magnetic field along a circle around the wire.
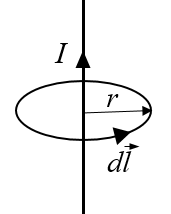
As the integration is performed around the loop, $d\vec{l}$ is parallel to $\vec{B}$ at every step. Since $|\vec{B}|$ is constant along the loop the result of the line integral is,
$$\oint\limits_{C}\vec{B}\cdot d\vec{l}=2\pi r |\vec{B}|.$$This yields the same formula for the magnetic field around a current carrying wire as was determined using the Biot-Savart law.
$$\bbox[10px, border: 1px solid black]{|\vec{B}(\vec{r})|=\frac{\mu_0I}{2\pi r}\hspace{1cm}\text{[T]}.}$$Arbitrary orientation
Consider a long straight wire with current $I$ flowing in the direction $\hat{n}$ that passes through the point $\vec{r}_0$. The vector pointing from $\vec{r}_0$ to some other point $\vec{r}$ is $\vec{r}-\vec{r}_0$. This vector can be decomposed into a distance along the wire and a distance perpendicular to the wire, $\vec{r}-\vec{r}_0 = \vec{d}_{\parallel} + \vec{d}_{\perp}$, where the parallel component is the projection of $\vec{r}-\vec{r}_0$ onto $\hat{n}$, $\vec{d}_{\parallel}=\hat{n}\cdot(\vec{r}-\vec{r}_0)\,\hat{n}$. The shortest distance from the wire to point $\vec{r}$ is $\vec{d}_{\perp}=(\vec{r}-\vec{r}_0)-\vec{d}_{\parallel}$.
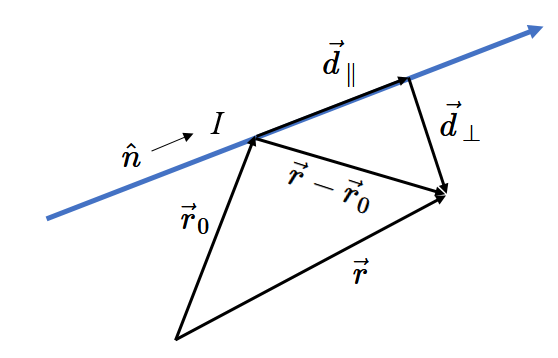
The magnetic field at point $\vec{r}$ due to the current flowing through this wire is,
$$\vec{B}(\vec{r})=\frac{\mu_0I}{2\pi|\vec{d}_{\perp}|}\,\hat{n}\times\hat{d}_{\perp}\,\,\text{[T]}.$$The direction of the magnetic field is given by the cross product of $\hat{n}$ (the direction the current is flowing) and $\hat{d}_{\perp}$ (the unit vector perpendicular to the wire that points towards point $\vec{r}$).