The magnetic field along the axis of a current loop
A current $I$ [A] flows in a circular wire of radius $R$ lies in the $x-y$ . To calculate the magnetic field along the $z$-axis, the Biot-Savart law can be used.
$$ d\vec{B}(\vec{r})=\frac{\mu_0}{4\pi}\frac{I d\vec{r}_{wire} \times (\vec{r}-\vec{r}_{wire})}{|\vec{r}-\vec{r}_{wire}|^3}\hspace{1cm}\text{[T]}.$$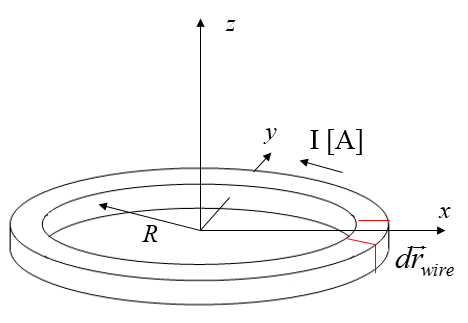
The contribution to the field of the wire segment $d\vec{r}$ along the $x$-axis is,
$$ d\vec{B}(\vec{r})=\frac{\mu_0}{4\pi}\frac{I dy\hat{y} \times (z\hat{z}-R\hat{x})}{\sqrt{R^2+z^2}^3}\hspace{1cm}\text{[T]}.$$$\hat{y}\times\hat{z}=\hat{x}$ and $\hat{y}\times\hat{x}=-\hat{z}$.
$$ d\vec{B}(\vec{r})=\frac{\mu_0}{4\pi}\frac{I dy (z\hat{x}+R\hat{z})}{\sqrt{R^2+z^2}^3}\hspace{1cm}\text{[T]}.$$The sum of the horizontal components from all the wire segments around the circle will add to zero so the field at position $z$ will be,
$$\vec{B}(z)=\frac{\mu_0}{4\pi}\frac{I 2 \pi R^2\hat{z}}{\sqrt{R^2+z^2}^3}=\frac{\mu_0I R^2\hat{z}}{2\sqrt{R^2+z^2}^3}\hspace{1cm}\text{[T]}.$$At large distances from the loop, the amplitude of the magnetic field falls like $\frac{1}{z^3}$.
If such loops are stacked on top of each other so that there are $n$ wire loops per meter, then the field can be calculated by summing the contributions from all of the loops.
$$\vec{B}(z) = \int\limits_{-\infty}^{\infty}\frac{\mu_0nI R^2dz}{2\sqrt{R^2+z^2}^3}\hat{z}\hspace{1cm}\text{[T]}.$$Using the identity,
$$\int\limits_{-\infty}^{\infty}\frac{dz}{\left(R^2+z^2\right)^{3/2}} = \frac{2}{R^2},$$yields the simple result,
$$\bbox[10px, border: 1px solid black]{\vec{B} = \mu_0nI \,\hat{z} \hspace{1cm}\text{[T].}}$$This is the result for the magnetic field inside a solenoid with $n$ windings per meter.
