Thin lenses: small angle approximation

By experimenting with the thick lens app we saw that it is possible to focus light to a point if only the light rays close to the optical axis are allowed to participate and if the lens is thin $(d << f)$. In this case it is convenient to measure the angles with respect to the horizontal optical axis. For small angles, the angle in radians is the slope of the light ray.

Consider a light ray striking an interface at a small angle to the optical axis.

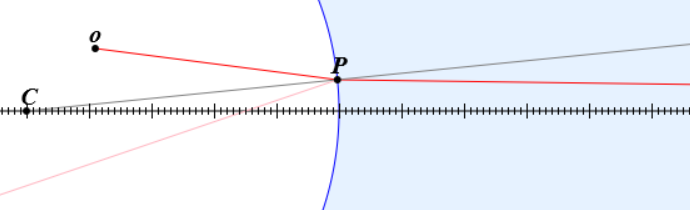
The slope of the ray to the left of the interface is,

The line $\overline{CP}$ is normal to the interface. If $|y_P| << |R|$, then the slope of the line normal to the interface is, $\phi_n \approx -\frac{y_p}{R}$. The angle between the incoming ray and the normal to the interface is,

Using Snell's law it is possible to calculate the angle the light ray makes to the normal to the interface on the right side.

Since $\phi_1$ and $\phi_n$ are small angles, $\theta_1$ and $\theta_2$ will be small angles too and we can use the approximation that $\sin(x)\approx x$. The simplified version of Snell's law is,

On the right side of the interface, the angle between the normal and the light ray, $\theta_2$ can be written in terms of the slope of the normal, $\phi_n$, and the slope of the light ray on the right side of the interface, $\phi_2$. $$ \theta_2 = \phi_2 - \phi_n\quad\text{rad}.$$

This equation can be solved for $\phi_2$. Using the simplified version of Snell's law,

This small angle approximation describes how a light ray with a small angle to the optical axis is bent at an interface. A lens consists of two interfaces so it is necessary to use this formula twice. Consider a lens with an index of refraction $n_{\text{lens}}$ in a medium with an index of refraction $n_{\text{env}}$. The lens has a radius $R_{\text{left}}$ on the left side and $R_{\text{right}}$ on the right side. The slope of the light ray to the left of the lens is $\phi_{\text{left}}$. We assume that this angle is small. Using the small angle approximation, the slope of the light ray after it strikes the left interface is,

$ \phi_{\text{lens}} $ is the slope of the ray inside the lens. The ray then strikes the right interface. We assume that the lens is so thin that the distance from the optical axis, $y_P$, remains the same. The slope of the light ray to the right of the lens is,

Substituting for $\phi_{\text{lens}}$ using the equation above yields,

This can be written more compactly as,

where $f$ is the focal length,

This is called the lens-maker's formula. Most of the time, lenses are used in air and $n_{\text{env}}=1$. The lens-maker's formula then simplifies to,

In the simulation below, light is emitted by an object $o$. There are three special light rays. The first is the ray that leaves the object horizontally, $\phi_{\text{left}}=0$. For this ray, the slope on the right of the lens is $\phi_{\text{right}} \approx -\frac{y_P}{f}$. For any value of $y_P$, this ray will pass through the focal point of the lens. This focal point is the blue point labeled $f$. The second special ray is the ray that leaves object $o$ and passes through the point $y_p=0$. For this ray $\phi_{\text{right}} \approx \phi_{\text{left}}$. This ray is not bent by the lens. The third special ray leaves object $o$ and passes through the mirror image of the focal point $f'$. This ray is bent horizontally so that $\phi_{\text{right}}=0$. All three of these special rays meet at the image point $i$.

The focal length can be both positive and negative. Converging lenses have a positive focal length which is to the right of the lens in the simulation. Diverging lenses have a negative focal length which is to the left of the lens. The image point is virtual if the rays do not pass through the image point and only the (pink) extensions of the rays on the right pass through the image point. The image is virtual if $f < 0$ or $f >0$ and $x_o$ is closer to the lens than a focal length.