Thick lens

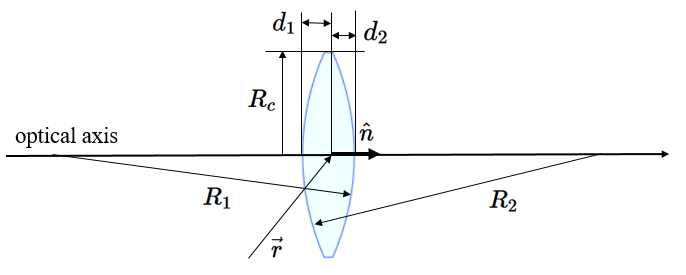
We consider a lens consisting of two spherical surfaces centered on an optical axis and one cylindrical surface where the central axis of the cylinder is along the optical axis. The radius of curvature of the left spherical interface is $R_1$, the radius of curvature of the right spherical interface is $R_2$, and the radius of the cylinder is $R_c$. The spherical surfaces intersect the optical axis at $d_1$ and $d_2$.

The view shown below is looking down at the $x-y$ plane. It is possible to rotate the optical axis of the lens an angle $\phi$ with respect to the $x-$axis. Light rays leave an object $(x_o,y_o)$ and are reflected and refracted at the interfaces. The reflected rays have 1/10 the intensity of the incident rays and the refracted rays have 9/10 the intensity of the incident rays. The refraction can be calculated using Snell's law of refraction at a spherical interface. The index of refraction is wavelength dependent and is modelled by a Cauchy law $n = A + B/\lambda^2$. The wavelengths used by the light sources are given in nanometers as a list in square brackets such as [450,510,650].

Lens types:

A three-dimensional version of this app is available here.

<form name="data_env">
<p>A lens is placed in a medium such as water or oil with an index of refraction greater than 1. The focal length of a lens changes it is placed in another environment with a different index of refraction. Press the buttons for 'Air', 'Water' and 'Immersion oil' to see this effect. Sometimes in a light microscope an immerion oil is used to try to collect more light and increase the resolving power of the microscope. The form below will let you change the index of refraction of the medium around the lens. </p>
<p style="text-align:center">$n_{\text{medium}} = A + B/\lambda^2$, $A=$ 
	  <input type="text" name="A_envi" value="1.33" size="10"/>, $B=$ 
	  <input type="text" name="B_envi" value="5200" size="10"/> [nm²]<br />
<input type="button" value="submit" onclick="A_env = parseFloat(data_env.A_envi.value); B_env = parseFloat(data_env.B_envi.value); update(); "/> <input type="button" value="Air" onclick="A_env = 1; data_env.A_envi.value = 1; B_env = 0; data_env.B_envi.value = 0;  update(); "/> <input type="button" value="Water" onclick="A_env = 1.33; data_env.A_envi.value = 1.33; B_env = 5200; data_env.B_envi.value = 5200;  update(); "/> <input type="button" value="Immersion oil" onclick="A_env = 1.515; data_env.A_envi.value = 1.515; B_env = 4500; data_env.B_envi.value = 4500;  update(); "/></p>
</form>






	Physik für Geodäsie 511.018 / Physik M 513.805