A mass on a frictionless table connected to two springs

Systems with more degrees of freedom can have different resonance frequencies for different modes. A normal mode of a system is one in which all components of the system oscillate with the same frequency. A simple example is a mass connected by two springs such that the oscillation frewquency for horizontal motion is different for the oscillation frequency for vertical motion. This is illustrated in the following video.

The trajectory of the mass can be calculated by numerically integrating the differential equation that describes this motion.

A mass $m$ on a frictionless horizonal table is connected to the left and to the right by two springs each with a spring constant $k$. The length of the unstretched springs is $l$ and the width of the table is $w > 2l$.

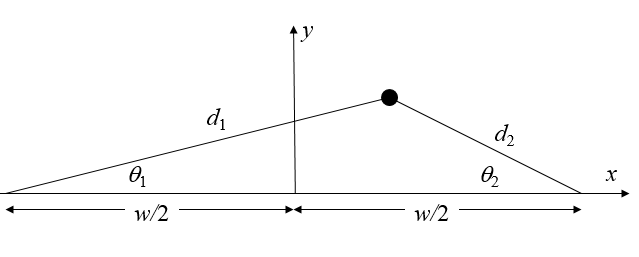
The equilibrium position for the mass is in the middle of the table $(x=0,y=0)$ where the forces exerted by the springs cancel each other out. If the mass is moved away from its equilibrium position then the force on on the mass is,

\[ \begin{equation} \vec{F}=k\left[(d_2-l)\cos\theta_2-(d_1-l)\cos\theta_1\right]\hat{x}-k\left[(d_2-l)\sin\theta_2+(d_1-l)\sin\theta_1\right]\hat{y}. \end{equation} \]

Here $d_1 = \sqrt{(w/2+x)^2+y^2}$, $d_2 = \sqrt{(w/2-x)^2+y^2}$, $\theta_1=\text{atan}\left(\frac{y}{w/2+x}\right)$, and $\theta_2=\text{atan}\left(\frac{y}{w/2-x}\right)$.

The form below will calculate the trajectory of the mass when it is released from postion $(x_0,y_0)$ at rest.

$m=$  kg $k=$  N/m $l=$  m $w=$  m $x_0=$  m $y_0=$  m

 Numerical 6th order differential equation solver 

$ \large \frac{dx}{dt}=$

$v_x$

$ \large \frac{dv_x}{dt}=$

$ \large \frac{dy}{dt}=$

$v_y$

$ \large \frac{dv_y}{dt}=$

$ \large \frac{dz}{dt}=$

$v_z$

$ \large \frac{dv_z}{dt}=$

Initial conditions: 

$t_0=$

 

$\Delta t=$

$x(t_0)=$

 

$N_{steps}$

$v_x(t_0)=$

 

Plot:

vs.

$y(t_0)=$

 

$v_y(t_0)=$

 

$z(t_0)=$

 

$v_z(t_0)=$

 

 
 

 $t$   $x$   $v_x$   $y$   $v_y$   $z$   $v_z$