Coupled oscillators

Coupled systems of masses exhibit different normal modes. A normal mode of a system is one in which all components of the system oscillate with the same frequency. Consider two masses confined to move in the $x$-direction connected by springs.

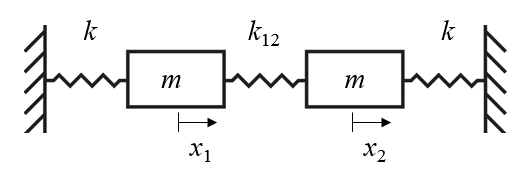
There are two normal modes of this system. In the first mode, the two masses move left and right together so that the spring $k_{12}$ is never compressed. In the second mode, the masses move out of phase, first towards each other and then away from each other. These two normal modes are illustrated in the video below.

Any motion of this system can be described as superposition of these two normal modes. The differential equations that describe this system are,

$$m\frac{d^2x_1}{dt^2}=-kx_1 -k_{12}(x_1-x_2)\\m\frac{d^2x_2}{dt^2}=-kx_2 -k_{12}(x_2-x_1)$$

These equations have been put into the differential equation solver below with the parameters $m=1$, $k=1$, $k_{12}=0.1$. There are buttons to set initial conditions to excite the in-phase mode $(v_1 = 1,\,v_2=1)$ and the out-of-phase mode $(v_1 = 1,\,v_2=-1)$. The out-of-phase mode has a slightly higher frequency than the in-phase mode. There is also a button to start the system in a superposition of the two modes. Since the frequencies of the two modes are nearly the same, they interfere constructively for smoe time and then destructively for some time. This phenomena is known as beats.

The trajectory of the mass can be calculated buy numerically integrating the differential equation that describes this motion.

 Numerical 6th order differential equation solver 

$ \large \frac{dx}{dt}=$

$v_x$

$ \large \frac{dv_x}{dt}=$

$ \large \frac{dy}{dt}=$

$v_y$

$ \large \frac{dv_y}{dt}=$

$ \large \frac{dz}{dt}=$

$v_z$

$ \large \frac{dv_z}{dt}=$

Initial conditions: 

$t_0=$

 

$\Delta t=$

$x(t_0)=$

 

$N_{steps}$

$v_x(t_0)=$

 

Plot:

vs.

$y(t_0)=$

 

$v_y(t_0)=$

 

$z(t_0)=$

 

$v_z(t_0)=$

 

 
 

 $t$   $x$   $v_x$   $y$   $v_y$   $z$   $v_z$