Refraction of waves

The direction that plane waves propagate changes at an interface where the wave velocity changes. This is called refraction. The following video is a simulation of waves which start out in a medium with a low wave velocity and enter a region with high wave velocity. In both regions the frequency of the waves is the same but there is a longer wavelength in the region with the higher wave velocity.

To understand why the waves change directions we consider plane waves striking an interface at an angle. The wave velocity is higher in the light blue region and lower in the dark blue region. This means that the wavelength in the light blue region is longer, $\lambda_1 > \lambda_2$.

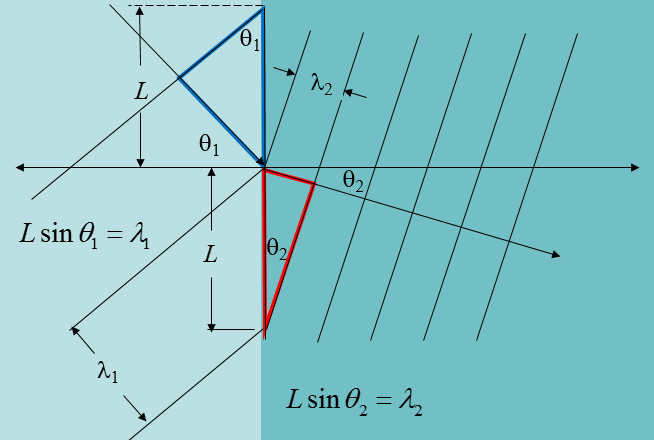
The thin black lines indicate the positons of the maxima of the plane waves. When a maximum arives from one side at the interface it must cause a wave maximum at that point on the other side. The only way to get all of the maxima to match at the interface with the two different wavelengths is to change the direction of propagation of the waves.

Let $L$ be the distance between the wave maxima along the interface. By examining the blue triangle we determine that $L\sin\theta_1=\lambda_1$ and by examining the red triangle we determine that $L\sin\theta_2=\lambda_2$. Solving both equations for $L$ we find,

This is a form of Snell's law. Since the frequency of the waves is the same on both sides and the wave velocity is $c=\lambda f$, Snell's law can also be written as,

When we are discussing light waves, the speed of light in a medium is the speed of light in vacuum $c_0$ divided by the index of refraction $n$ of that medium. For light, Snell's law can be written,