Single slit experiment

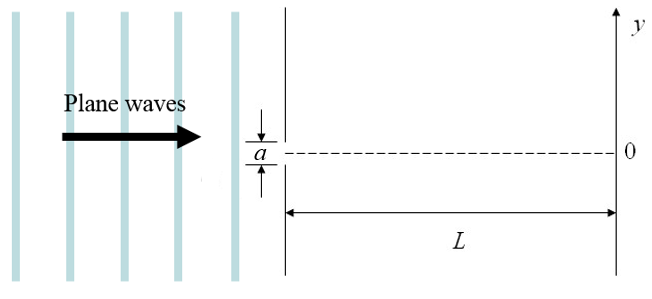
In a single slit experiment, waves pass through a narrow slit of width $a$ which is wider than the wavelength $\lambda$. The interference pattern is observed on a screen that is a distance $L$ from the slit.

$a$

= 100 μm

$L$

= 2 m

$\lambda$

= 650 nm
$y$ mouse position =   mm

The small divisions on the scale on the right represent mm.

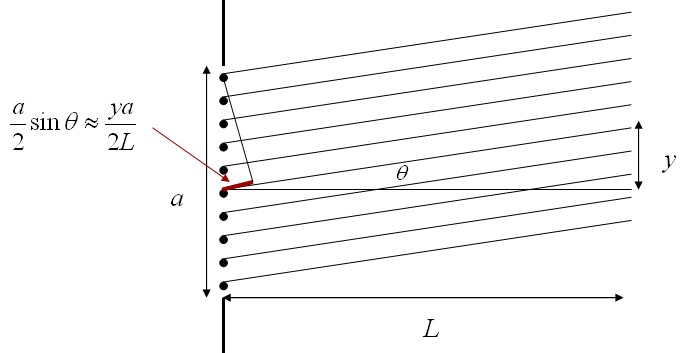
  Your browser does not support the canvas element.

A single slit can be thought of as consisting of many small sources. This is called the Huygens principle.. These sources are represented by the dots in the diagram. The amplitude of the waves from each of the small sources is $\frac{E_0}{a}dy$. The waves from each of the sources will have a different phase when they arrive at the screen depending on the angle $\theta$. This phase is $-2\pi y\sin (\theta)/\lambda = -\beta y/a$, where $\beta$ is a constant, $\beta = 2\pi a \sin(\theta)/\lambda$. The contributions to the total amplitude from all of the sources is given by the following integral.

$$E=\frac{E_0}{a}\int\limits_{-a/2}^{a/2}e^{i\omega t +i\beta y/a}dy.$$

Performing the integration gives,

$$E=\frac{E_0}{i\beta}e^{i\omega t}\left( e^{i\beta /2} - e^{-i\beta /2}\right) = \frac{E_0}{\beta/2}e^{i\omega t}\sin (\beta /2).$$

The squared amplitude is,

$$|E|^2=E^*E= \frac{E_0^2}{(\beta/2)^2}\sin^2 (\beta /2).$$

Since the intensity is proportional to the squared amplitude,

$$I=I_0 \frac{\sin^2 (\beta /2)}{(\beta /2)^2}.$$
$\frac{I}{I_0}$

$y$ [m]

Far field

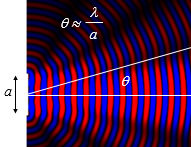
In the far field, where $L > > \lambda$ and $L > > y$, destructive interference will take place when $n\lambda=\frac{ay}{L}$ where $n$ is an integer, $n\ne 0$. The first minimum is for $n=1$. If the slit is wide compared to the wavelength, then in the far field, the central maximum diverges with an angle $\theta \approx \frac{\lambda}{a}$.

Frage