Conservation of energy

Energy is conserved. It can be exchanged between the forms of kinetic energy, potential energy, or thermal energy but the total energy remains the same. The kinetic energy of a particle is, $E_{kin} = \frac{mv^2}{2}$ [J] where $m$ [kg] is the mass of the particle and $v$ [m/s] is its velocity.

The work performed equals the change in kinetic energy plus the change in potential energy plus the work performed against any nonconservative (frictional) forces.

Example 1

A mass of 500 g is placed on a frictionless table and is attached to a nonlinear spring. The force that the spring exerts is $F=-6x-4x^3$ [N] where $x$ is measured in meters. The spring is compressed 16 cm and then released such that the initial velocity of the mass is zero. What is the maximum velocity of the mass?

Solution: Potential energy is stored in the spring by compressing it. This energy is $W = \int Fdx = \int\limits_0^{0.16} 6x+4x^3 dx = \left. 3x^2 + x^4\right|_0^{0.16}=0.07745536$ [J]. Because there is no friction, all of this energy is converted into kinetic energy $\frac{mv^2}{2}$. The maximum velocity is $v_{max} = 0.5566$ [m/s].

Example 2

A box with a mass of 14 kg pulled 5 m across a horizontal floor by pulling on a rope at an angle of 45° with a force of 72 N. The initial kinetic energy of the box is zero and the final kinetic energy of the box is zero. As the box is pulled across the floor, frictional forces generate heat. How much thermal energy is created by dragging this box across the floor?

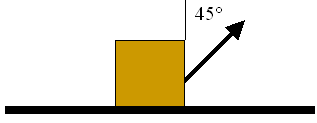
Solution: The change in kinetic energy is zero and the change in potential energy is zero so the work required to move the box is entirely converted into thermal energy. The mass of the box is not relevant.