Power

Power $P$ is the work that is exerted per unit time,

$$ P = \frac{dW}{dt}\hspace{1cm}\text{[W]}.$$

the units of power are Watts, W = J/s. In the last section it was shown that,

$$W = \int\limits_{t_1}^{t_2}\vec{F}(t)\cdot \vec{v}(t)dt.$$

Differentiating both sides we see that the power can also be expressed as,

$$P = \vec{F}(t)\cdot \vec{v}(t).$$

Example 1

A box with a mass of 14 kg pulled across a horizontal floor by pulling on a rope at an angle of 45° with a force of 72 N. How much power is needed to move the box with a constant velocity of 0.2 m/s?

Solution: $P = \vec{F}(t)\cdot \vec{v}(t).$  

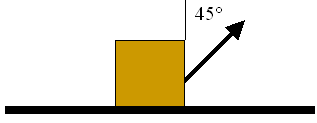
Example 2

Consider a damped mass-spring system which moves along the $x$-axis. A mass of 1 kg is attached to a linear $F_{\text{spring}}= -kx$ and there is a drag force that is in the opposite direction as the velocity, $F_{\text{drag}}= -0.4v_x$. The mass is given an initial velocity in the positive $x$-direction while its initial position is $x=0$ and the spring is not initially compressed. The trajectory is,

$$x(t)= e^{-0.2t}\sin(t).$$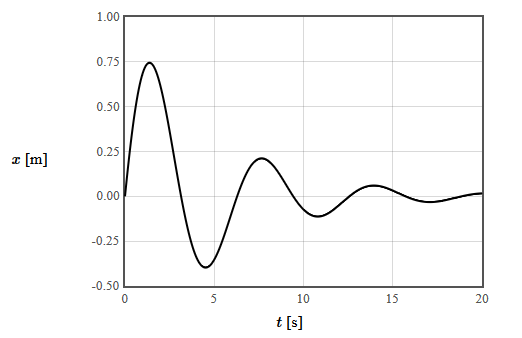

The velocity is,

$$v_x(t)= e^{-0.2t}\left( \cos(t) - 0.2\sin(t)\right).$$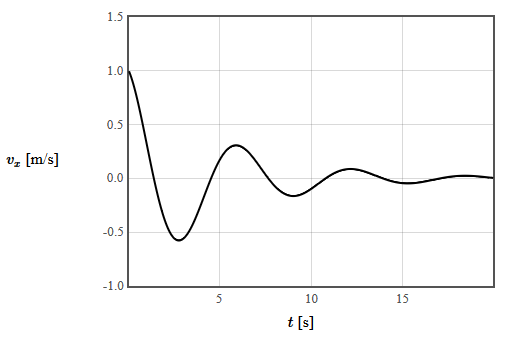

At $t=0$ the initial velocity is $v_x = 1$.

The acceleration is,

$$a_x(t)= -e^{-0.2t}\left( 0.96\sin(t) + 0.4\cos(t)\right).$$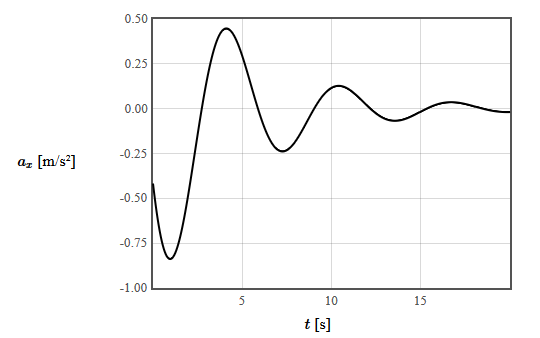

Since $m=1$ kg, the force is $F_x= -e^{-0.2t}\left( 0.96\sin(t) + 0.4\cos(t)\right) = -kx -0.4v_x$. As $x$ and $v_x$ are known, this can be solved for the spring constant $k= 1.04$ N/m.

The power provided by the spring is $F_{\text{spring}}v_x = -kxv_x = -1.04e^{-0.4t}\sin(t)\left(\cos(t)-0.2\sin(t)\right)$.

Notice how the power is first negative and then positive. Initially, the spring is compressed by the moving mass. The power is negative when energy is being stored in the spring. Later when the spring is expanding and increasing the kinetic energy of the mass, the power delivered by the spring is positive. The work performed by the spring is shown below. After the oscillations have decayed away, the total work performed by the spring is zero. No net work can be performed by a spring that was initially uncompressed and no energy is stored in the spring after the oscillations have decayed away.

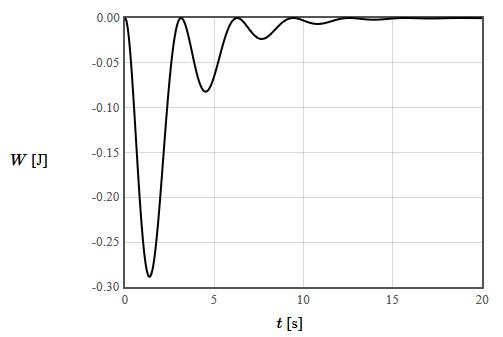
Next consider the power and the work of the drag force, $F_{\text{drag}}= -0.4v_x= -0.4e^{-0.2t}\left( \cos(t) - 0.2\sin(t)\right)$. The power delivered by this force is $P= -0.4v_x^2= -0.4e^{-0.4t}\left( \cos(t) - 0.2\sin(t)\right)^2$. This power is always negative. The drag force never provides energy to the mass, it always extracts energy. The work performed by the drag force is shown below.

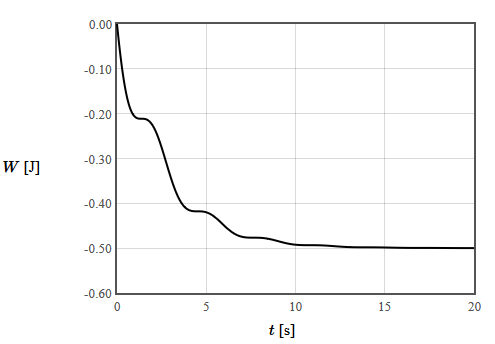
After the oscillations have damped out, the drag force has perfomed -0.5 J of work. This equals the intitial kinetic energy of the mass, $\frac{1}{2}mv_x^2 = 0.5$ J.

$P=$  [W]
in the range from $t_1=$  [s] to $t_2=$  [s].

 $t$   $P$ [W]

  

$P$ [W]

$t$ [s]

The work is,

$W=\int\limits_{t_1}^{t_2} P dt +W(t_1)$.

Here $W(t_1)$ is the integration constant. It is the work that was performed before time $t_1$.

$W(t_1)=$

 $t$ [s]  $W(t)$ [J]
  

$W$ [J]

$t$ [s]

Questions