Work performed by moving along a trajectory

Sometimes we need to determine the that is performed when a particle follows a specific trajectory,

$$\vec{r}(t) = r_x(t)\hat{x}+ r_y(t)\hat{y}+ r_z(t)\hat{z}.$$

From the position vector it is possible to determine the velocity vector,

$$\vec{v}=\frac{d\vec{r}}{dt}=\frac{dr_x}{dt}\hat{x}+ \frac{dr_y}{dt}\hat{y}+ \frac{dr_z}{dt}\hat{z}.$$

The force acting on this particle may have several contributions. It could be that an electrical force, a gravitational force, and a drag force all act on the particle. In general, these forces can be functions of position, velocity, and the time, $\vec{F}(\vec{r},\vec{v},t)$. For instance, a drag force is a function of the velocity and a gravitational force is a function of position. If the trajectory is known, then the position and the velocity are known as a function of time an the force can be expressed as only a function of time. The work is,

\begin{equation} W = \int\limits_{\vec{r}_1}^{\vec{r}_2}\vec{F}(t)\cdot d\vec{r}\hspace{1cm}\text{[J]}. \end{equation}

It is convenient to write $d\vec{r} = \vec{v}dt$. Then the integral for the work is,

$$W = \int\limits_{t_1}^{t_2}\vec{F}(t)\cdot \vec{v}(t)dt\hspace{1cm}\text{[J]}.$$ $$W = \int\limits_{t_1}^{t_2}\left( F_x(t)v_x(t) + F_y(t)v_y(t) + F_z(t)v_z(t)\right)dt\hspace{1cm}\text{[J]}.$$

Example 1

A particle moves in a viscous liquid following a hypocycloid,

$$\vec{r} = \left(5\cos (t) + \cos(5t) \right)\hat{x} + \left(5\sin (t) + \sin (5t) \right)\hat{y}.$$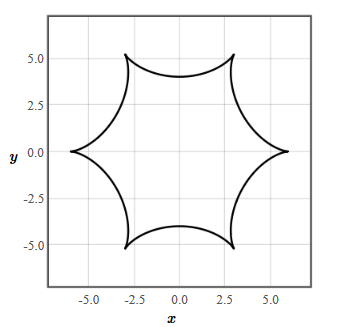

The drag force on this particle is in the opposite direction as the velocity, $\vec{F}_{\text{drag}}= -0.1\vec{v}$ [N]. To calculate the work, we must first determine the velocity vector,

$$\vec{v} = \left(-5\sin (t) - 5\sin(5t) \right)\hat{x} + \left(5\cos (t) + 5\cos (5t) \right)\hat{y}.$$

The force that moves the particle is in the opposite direction as the drag force, $\vec{F}=-\vec{F}_{\text{drag}}= 0.1\vec{v}$. The work is,

$$W = \int\limits_{t_1}^{t_2}\vec{F}(t)\cdot \vec{v}(t)dt = 0.1 \int\limits_{t_1}^{t_2}\left(\left(-5\cos (t) - 5\cos(5t) \right)^2 + \left(5\sin (t) + \sin (5t) \right)^2\right) dt. $$

It is possible to perform this integral but it is a lot of work and it would be easy to make a mistake. There are three methods we can use to find the solution: integrate with pencil and paper, use a symbolic integration program like Wolfram Alpha, or perform a numerical integration. It would be best to use at least two methods and check that all methods agree.

Wolfram Alpha provides the answer,

$$W = \left. 0.1 \frac{25}{2}\left(4t +\sin(4t)\right)\right|_{t_1}^{t_2}$$

For $t_1 = 0$ and $t_2 = 3$, $W = 14.329$ [J]. The form below will integrate a $\vec{F}\cdot\vec{v} = F_xv_x+F_yv_y+F_zv_z$ numerically. This numerical integration also yields $W = 14.329$ [J].

$\vec{F}\cdot\vec{v}=$  [J/s]
in the range from $t_1=$  [s] to $t_2=$  [s].

 $t$   $\vec{F}\cdot\vec{v}$

  

$\vec{F}\cdot\vec{v}$

$t$ [s]

The work is,

$W=\int\limits_{t_1}^{t_2} \vec{F}\cdot\vec{v} dt +W(t_1)$.

Here $W(t_1)$ is the integration constant. It is the work that was performed before time $t_1$.

$W(t_1)=$

 $t$ [s]  $W(t)$ [J]
  

$W$ [J]

$t$ [s]

Questions