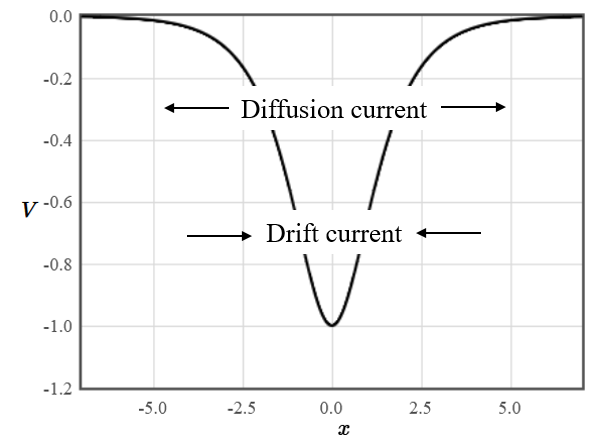
One of the remarkable papers that Einstein published in 1905 was about Brownian motion. In it, he considered what happens to charged particles confined to a region of space by an electrostatic potential $V$. The force on the particles will be $\vec{F}=-q\nabla V= q\vec{E}$ and they will be pulled to this minimum of the potential. Here $q$ is the charge of the particles and $\vec{E}$ is the electric field. This will cause a high concentration of particles at the minimum and they will diffuse away from the minimum. In equilibrium, there must be a balance between the inward current due to the attractive potential and the outward current due to diffusion.

The current density is,
$$\vec{j} = qn\mu\vec{E} - qD\nabla n.$$Here $n$ is the particle density, $\mu$ is the mobility of the particles, $q$ is the charge of the particle, and $D$ is the diffusion constant. Since the current density must be zero in equilibrium we have,
$$n\mu\vec{E} = D\nabla n.$$Einstein used Boltzmann's theory to argue that the particle density should be described by a Boltzmann factor,
$$n = n_0\exp\left(\frac{-qV}{k_BT}\right).$$The gradient of the particle density would then be,
$$\nabla n = -\frac{n_0q}{k_BT}\nabla V\exp\left(\frac{-qV}{k_BT}\right)= -\frac{q\nabla V}{k_BT}n.$$substituting this into the equation for the balance between the drift and diffusion currents and using the fact that $\vec{E}=-\nabla V$ yields,
$$\bbox[10px, border: 1px solid black]{\mu = \frac{qD}{k_BT}.}$$This is known as the Einstein relation. It says that particles with a high diffusion constant will have a high mobility.
Next, consider an n-type semiconductor. The total electron current density is,
$$\vec{j}_n=en\mu_n\vec{E} + eD_n\nabla n.$$The electric field is proportional to the gradient of the conduction band edge $e\vec{E} = \nabla E_c$, and the electron density depends on the position of the conduction band with respect to the Fermi energy, $n = N_c\exp\left(\frac{E_F - E_c}{k_BT}\right)$. If the semiconductor is in equilibrium, the Fermi energy is constant and
$$\nabla n = -\frac{\nabla E_c}{k_BT}N_c\exp\left(\frac{E_F - E_c}{k_BT}\right)=-\frac{\nabla E_c}{k_BT}n.$$Substituting these into the expression for the current density yields,
$$\vec{j}_n=n\nabla E_c\left(\mu_n - \frac{eD_n}{k_BT}\right).$$The quantity in brackets is the Einstein relation. This means that the current density in a semiconductor where the Fermi energy is constant is zero. The drift current is always balanced by the diffusion current.