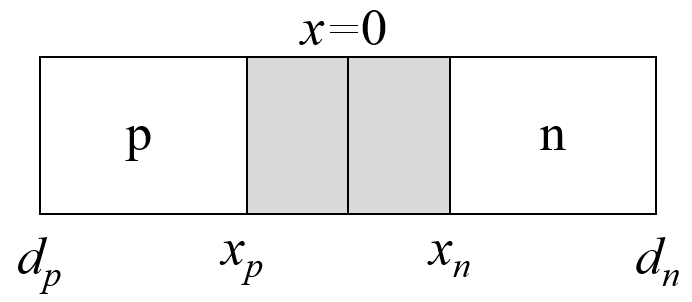
In a forward-biased pn-junction, electrons are injected into the p-side as minority carriers, and holes are injected into the n-side as minority carriers. The concentrations of the minority carriers diffuse away from the junction due to recombination. This establishes a concentration gradient of minority electrons on the p-side and a concentration gradient of minority holes on the n-side. A diffusion current flows because of the concentration gradients.
Let $d_p$ be the position of the metal-semiconductor interface on the p-side, $x_p$ be the edge of the depletion region on the p-side, $x_n$ be the edge of the depletion region on the n-side, and $d_n$ the position of the metal-semiconductor interface on the n-side. The junction between n and p is located at $x = 0$. The gray regions represent the depletion zones.
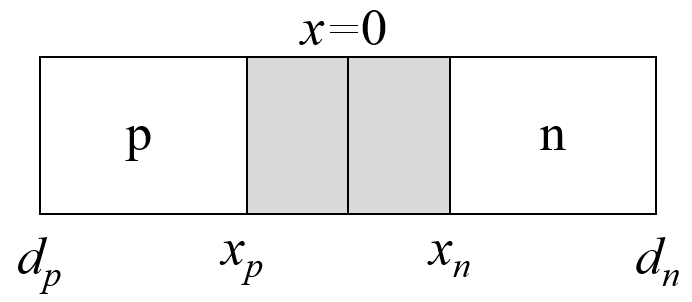
The minority carrier concentrations at the boundaries are,
$$n_p(d_p) = n_{p_0},\qquad n_p(x_p)=n_{p_0} \exp \left(\frac{eV}{k_BT}\right),\qquad p_n(x_n)=p_{n_0} \exp \left(\frac{eV}{k_BT}\right),\qquad p_n(d_n)=p_{n_0}.$$Here $V$ is the bias voltage, $T$ is the absolute temperature, $e$ is the elementary charge, and $k_B$ is Boltzmann's constant. Due to the many defects at the metal-semiconductor interface, the minority carrier concentrations return to the equilibrium carrier concentrations $n_{p_0}=n_i^2/N_A$ on the p-side and $p_{n_0}=n_i^2/N_D$ on the n-side at the interface.
Generally, the carrier concentrations are described by the continuity equations,
$$\frac{\partial p}{\partial t} = -p \mu_p \nabla \cdot \vec{E} - \nabla p \mu_p \vec{E} + D_p \nabla^2 p + G_p - R_p\\ \frac{\partial n}{\partial t} = n \mu_n \nabla \cdot \vec{E} + \nabla n \mu_n \vec{E} + D_n \nabla^2 n + G_n - R_n.$$However, in the part of the semiconductor that is not depleted, the electric field is negligible, if no light falls on the diode the generation terms are zero $(G_n =G_p = 0)$, and for steady-state conditions $\left( \frac{\partial n}{\partial t} = \frac{\partial p}{\partial t} =0\right)$ so the continuity equations simplify to the diffusion equations with a recombination term.
$$D_n \frac{\partial ^2 n_p}{\partial x^2}=\frac{n_p-n_{p_0}}{\tau _n}, \qquad D_p \frac{\partial ^2 p_n}{\partial x^2}=\frac{p_n-p_{n_0}}{\tau _p}.$$Here $D_n$ and $D_p$ are the diffusion constants for electrons and holes while $\tau_n$ and $\tau_p$ are the minority carrier lifetimes for electrons and holes.
The general solutions of the diffusion equations have the form:
$$n_p(x)= n_{p_0} + A_n\exp \left(\frac{-x}{L_n}\right) + B_n\exp \left(\frac{x}{L_n}\right), \quad \text{for} \quad d_p < x < x_p$$ $$p_n(x)= p_{n_0} + A_p\exp \left(\frac{-x}{L_p}\right) + B_p\exp \left(\frac{x}{L_p}\right), \quad \text{for} \quad x_n < x < d_n$$The boundary conditions can be used to determine the constants $A$ and $B$.
$$A_n = \frac{n_{p_0}\left(\exp\left(\frac{eV}{k_BT}\right)-1\right)\exp \left(\frac{-x_p}{L_n}\right)}{\exp \left(\frac{-2x_p}{L_n}\right) - \exp \left(\frac{-2d_p}{L_n}\right)},\qquad B_n = \frac{n_{p_0}\left(\exp\left(\frac{eV}{k_BT}\right)-1\right)\exp \left(\frac{x_p}{L_n}\right)}{\exp \left(\frac{2x_p}{L_n}\right)-\exp \left(\frac{2d_p}{L_n}\right)}.$$ $$A_p = \frac{p_{n_0}\left(\exp\left(\frac{eV}{k_BT}\right)-1\right)\exp \left(\frac{-x_n}{L_p}\right)}{\exp \left(\frac{-2x_n}{L_p}\right) - \exp \left(\frac{-2d_n}{L_p}\right)},\qquad B_p = \frac{p_{n_0}\left(\exp\left(\frac{eV}{k_BT}\right)-1\right)\exp \left(\frac{x_n}{L_p}\right)}{\exp \left(\frac{2x_n}{L_p}\right)-\exp \left(\frac{2d_n}{L_p}\right)}.$$The diffusion lengths $L_n = \sqrt{D_n \tau_n}$ and $L_p = \sqrt{D_p \tau_p}$ describe how the minority carrier concentrations decay through recombination. The diffusion current densities are,
$$j_{diff,n} = e D_n \frac{dn}{dx} = \frac{e D_n}{L_n} \left(-A_n\exp \left(\frac{-x}{L_n}\right) + B_n\exp \left(\frac{x}{L_n}\right) \right ), \quad \text{for} \quad d_p < x < x_p$$ $$j_{diff,p} = - e D_p \frac{dp}{dx} = \frac{e D_p}{L_p} \left(A_p\exp \left(\frac{-x}{L_p}\right) - B_p\exp \left(\frac{x}{L_p}\right) \right ), \quad \text{for} \quad x_n < x < d_n$$The total current density is the sum of the electron current density evaluated at $x_p$ and the hole current density evaluated at $x_n$.
$$j_{diff} = j_{diff,n}(x_p)+j_{diff,p}(x_n).$$$E_g=$ eV $W=|x_n|+|x_p|=$ μm $x_p=$ μm $x_n=$ μm $V_{bi}=$ V $n_i=$ cm-3
$D_p=$ cm²/s $D_n=$ cm²/s $L_p=$ μm $L_n=$ μm $n_{p_0}=$ cm-3 $p_{n_0}=$ cm-3
$A_n=$ cm-3 $B_n=$ cm-3 $A_p=$ cm-3 $B_p=$ cm-3
$j_n=$ A cm-2 $j_p=$ A cm-2 $j_{\text{diff}}=$ A cm-2
|
Minority Carrier Densities
|
log10(Minority Carrier Densities)
|
p-side (minority electrons) |
n-side (minority holes) |