Introduction

Power diodes are fundamental components in electronic circuits, renowned for their capability to handle high currents and voltages. The performance and efficiency of these diodes are significantly influenced by temperature, which affects their I-V (current-voltage) characteristics. Understanding the temperature dependence of these characteristics is crucial for designing robust and reliable electronic systems.
This lab aims to measure the temperature-dependent I-V characteristics of a power diode. Discrepancies often arise between the calculated and measured I-V curves. By analyzing the measured curves in a semilogarithmic diagram (semilogy), the non-ideality factor (n) can be determined in two distinct regions of the measured curve, which deviate from the theoretical predictions. These regions correspond to the recombination and diffusion components of the current. Accurately identifying and understanding these regions are essential for improving the accuracy of diode models and enhancing the design of electronic systems.

Determining the non-ideality factor n

The shape of of an I-V curve of a diode can be describe by the Shockley diode equation. It is named after transistor co-inventor William Shockley and it models the exponential current-voltage (I-V) relationship in moderate constant current forward bias or reverse bias. For more information on the Shockley equation, see Shockley diode equation/wiki. The Shockley equation is given by:

$$I = I_{S} ( e^{\frac{V}{nV_T}} - 1 ) $$

I: The diode current.
I_S: The reverse saturation current.
V: The voltage across the diode.
n: The ideality factor, a number between 1 and 2 that typically accounts for the deviation from the ideal p-n junction behavior.
V_T: The thermal voltage, given by $ V_T = \frac{kT}{q} $, where:
- k: Boltzmann's constant ($1.38 \times 10^{-23} \, \text{J/K}$).
- T: Absolute temperature in Kelvin.
- q: Charge of an electron ($1.602 \times 10^{-19} \, \text{C}$).

The following plot shows the theoretically predicted IV curve of a diode according to the Shockley equation. The graph is taken from PN diode IV characteristics.

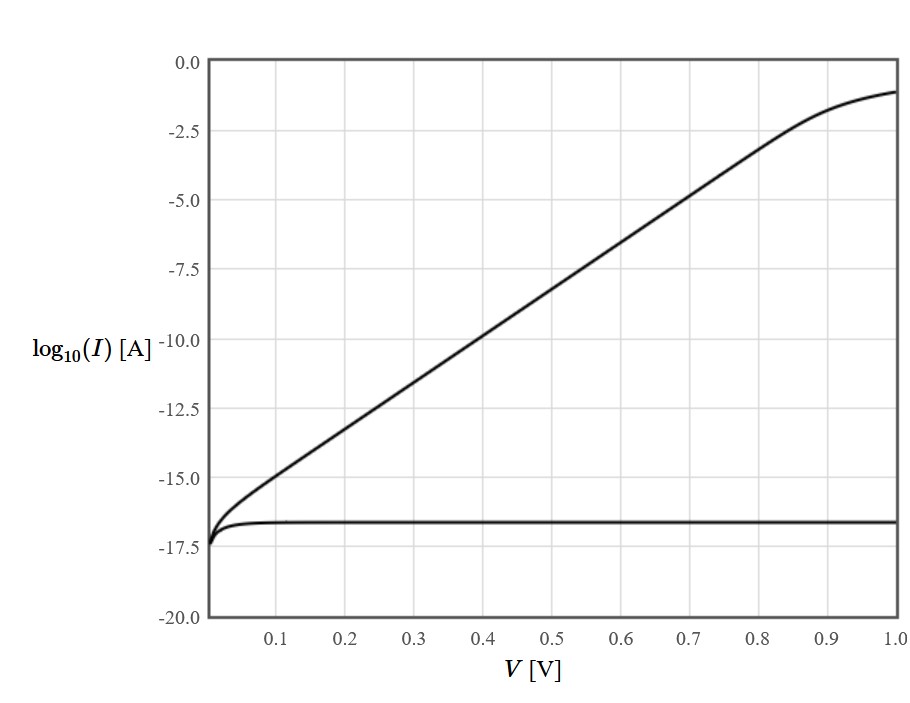
The IV curve graph displays the voltage (V) on the x-axis and the logarithm of the current (log_10(I)) on the y-axis. The upper line represents the forward bias region of the diode, showing an linear (exponential in cartesian coordinates) increase in current with increasing voltage. The lower line represents the reverse saturation current, which remains nearly constant and very low when the diode is reverse-biased.

In the experiment, the I-V curve is measured for different temperatures between 10 and 40 °C. This is done by connecting the power diode in forward bias to channel A of the Keithley 2600 Series Sourcemeter, applying a voltage between 0 and 0.6 volts, and measuring the resulting current. The setup is then placed in the climate chamber for proper temperature control. This experimental setup is controlled by the Python code shown in the text area at the end of this section.
The non-ideality factor n is determined in the lower voltage range from 0.02 V to 0.08 V and for 0.2 V to 0.4 V. This is done by fitting the curve with an exponential fit in the respective regions. The python code for calculating the fit can be seen in the second text area in the Appendix. The following two plots show the results of the two fits and the measured data.

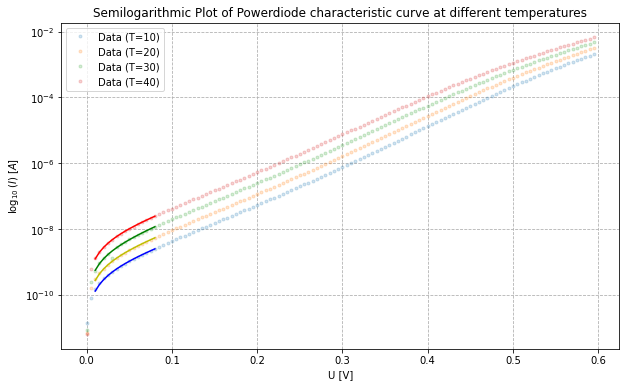
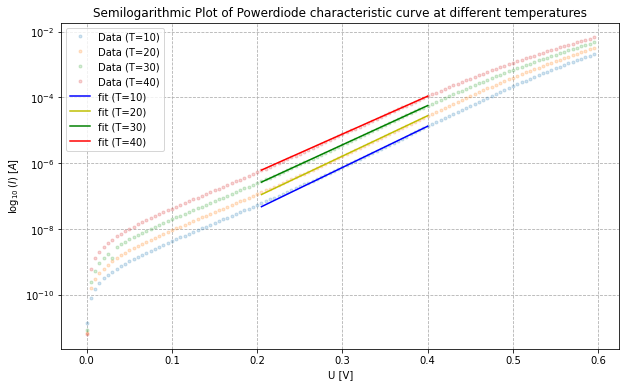
It can be seen that in the lower region the fit does not give a linear slope. This can be explained by the dominance of the -1 term in the Shockley equation. Theoretically, the recombination mechanism contributes more to the current in this region resulting in a theoretical non-ideality factor of 2. The second region refers to the diffusion mechanism, which should be dominant at higher voltages since it is the main mechanism of current through a diode. Theoretically the non-ideality factor in this region should be 1. The following table shows the non-ideality factors of the two fits. As we can see the results of the fit in the recombination region $n_l$ corelate for low temperature but deviate more and more for increasing temperatures. On the other hand the values for the diffusion region $n_h$ stay almost stable with increasing temperature but deviate from the prediction.

Data Table
T	n_l	n_h
10	1.91242226	1.42078510
20	1.79655436	1.40100056
30	1.63124279	1.39558203
40	1.68145189	1.39904020

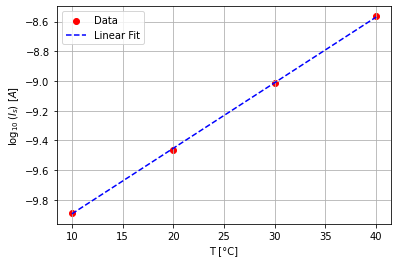
The reverse saturation current $I_s$ also can be determined by using the exponential fit. The values for the reverse saturation current can be used to show the dependancy of the $I_s$ to the temperature T. The following plot shows, that there is an exponential connection between those values. This makes sense since the reverse saturation current is dependent on the intrinsic carrier concentration $n_i$ which itself is an exponential function of the temperature. The values for the (See PN diode IV characteristics)

Temperature-Dependent Reverse Saturation current

Fitting the characteristic curve with a modified Shockley Equation

To get an accurate fit of the whole curve a modification of the Shockley equation is used. For this two terms of the original equation are added up with two independent saturation currents $I_s$. The double exponential Shockley equation is given by:

$$ I = I_{s1} \left( e^{\frac{V}{n_1 V_T}} - 1 \right) + I_{s2} \left( e^{\frac{V}{n_2 V_T}} - 1 \right) $$

where:

$ I $ is the diode current
$ I_s $ is the reverse saturation current
$ V $ is the voltage across the diode
$ n_1 $ and $ n_2 $ are non-ideality factors
$ V_T $ is the thermal voltage

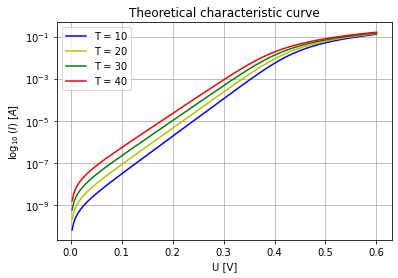
The theoretical plot is calculated using the program from PN diode IV characteristics and than ploting the resulting data with a python program. Since there is no knowledge about the measured Power diode, certain parameters have to be guessed. To get the best matching result we use the Germanium preset for the calculation. In the following plot we can see that there is a strong similarity. It has to be noticed though, that the theoretical curve has a hihger slope.

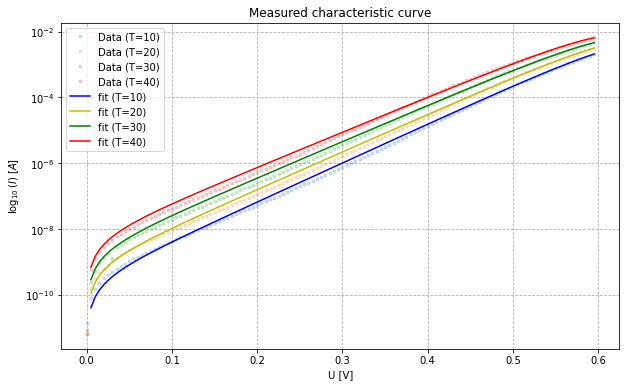
The following table shows the fit parameters of the modified double exponential Shockley equation. Using these parameters in combination with the Python code for the double exponential fit in the first text area of the Appendix, we obtain the plot of Figure 5.

Parameters of the double exponential Shockley equation fit
T[°C]	n₂	n₁	I_s2[A]	I_s1[A]
10	1	1.5	-3.0121e-14	2.8156e-10
20	1	1.5	-1.3123e-13	8.0865e-10
30	1	1.5	-5.0413e-13	2.1585e-09
40	1	1.5	-1.7186e-12	5.3308e-09

In the text area below is the Python code used to generate the data for the temperature dependent IV curves. The Keithley 2600 Python library is used to communicate with the sourcemeter, the voetsch.py is used to communicate with the climate chamber and the eLabFTW_config_api2_semilab library is used to upload the acquired data directly to the ELAB page. These libraries have to be in the same directory as the used Python code. Below the text area the python code and the measured datas are linked.

from KeithleyV15 import SMU26xx
import matplotlib.pyplot as plt
import time
import datetime
import csv
import numpy as np

#for use of ELABFTW
import os
import elabapi_python
import eLabFTW_config_api2_semilab as eLab
import json

from voetsch import VT4002

ip_address = "129.27.158.42"
username = "simpacuser"   # fill in the username on the front of the climate chamber
password = "u1s2e3r4" 



# connect to the climate chamber
climate_chamber = VT4002(ip_address, username, password)
climate_chamber.enable()
"""
EXAMPLE: characteristic curve of a diode

Schematic:

    --------------
    |            |
  -----         -|-
  | A | SMU     \|/
  -----         -|-
    |            |
    --------------

"""

""" ******* Connect to the Sourcemeter ******** """

# initialize the Sourcemeter and connect to it
# you may need to change the IP address depending on which sourcemeter you are using
sm = SMU26xx("TCPIP0::129.27.158.13::inst0::INSTR")

# get one channel of the Sourcemeter (we only need one for this measurement)
smu = sm.get_channel(sm.CHANNEL_B)

""" ******* Configure the SMU Channel A ******** """
#define a variable "current range" to be able to change it quickly for future measurements




# reset to default settings
#smu.reset()
# setup the operation mode of the source meter to act as a voltage source - the SMU generates a voltage and measures tcurrent
#smu.set_mode_voltage_source()
# set the voltage and current parameters
#smu.set_voltage_range(20)
#smu.set_voltage_limit(20)
#smu.set_voltage(0)
#smu.set_current_range(current_range)
#smu.set_current_limit(current_range)
#smu.set_current(0)

""" ******* For saving the data ******** """

#some suggestions for improvement of the data saving
    #the file name should identify the file uniquely
    #therefore specifying for example the voltage range, and the
    #type of characteristic (U/I, U/R, etc...) is suggested

# Create unique filenames for saving the data
time_for_name = datetime.datetime.now().strftime("%Y_%m_%d_%H%M%S")


# define the title of your experiment, under this name the experiment will be stored in ElabFTW
exp_title = "PowerdiodeTemperature"



#initializing a CSV file, to which the measurement data will be written - if this script is used to measure anothcharacteristic than the U/I curve, this has to be changed
# Header for csv


""" ******* Make a voltage-sweep and do some measurements ******** """

#some suggestions for the improvement of the measurement process
    #it would be nice to have a primary measurement, in which the
    #type of junction was be determined and a parameter was set
    #that indicated the forward direction of the junction
    #this primary measurement could also be executed and inlcuded
    #in the file name
    #this procedure would spare us the time of finding the forward
    #direction

# define sweep parameters
sweep_start = 0
sweep_end = 0.6
sweep_step = 0.005
steps = int((sweep_end - sweep_start) / sweep_step)
temperature = np.array([10,20,30,40])
overall_current_range = np.array([1e-1,1e-2,1e-3,1e-4,1e-5,1e-6,1e-7,1e-8])


# define variables we store the measurement in
# rename if needed




for sweep in range(len(temperature)):
    
    climate_chamber.go_to_temperature(temperature[sweep], 0.2, 60)
    time.sleep(300)
   
   

  

    

    
    for cu in range(len(overall_current_range)):
        # reset to default settings
        smu.reset()
        
        # enable the output
        smu.enable_output()
        #setup the operation mode of the source meter to act as a voltage source - the SMU generates a voltage and measures tcurrent
        smu.set_mode_voltage_source()
        current_range = overall_current_range[cu]


        current_range_for_name = str(current_range)
    
        # set the voltage and current parameters
        smu.set_voltage_range(2)
        smu.set_voltage_limit(2)
        smu.set_voltage(0)
        smu.set_current_range(current_range)
        smu.set_current_limit(current_range)
        
        # step through the voltages and get the values from the device
        filename_csv = 'Diode_' + 'temperature' + str(temperature[sweep]) + '_currentrange' + current_range_for_name +'.csv'
        filename_pdf = 'Diode_' + 'temperature' + str(temperature[sweep]) + '_currentrange' + current_range_for_name +'.pdf'
        with open(filename_csv, 'a') as csvfile:
            writer = csv.writer(csvfile, delimiter=';',  lineterminator='\n')
            writer.writerow(["Voltage / V", "Current / A"])
        data_current = []
        data_voltage = []
        
        
        for nr in range(steps):
            # calculate the new voltage we want to set
            voltage_to_set = sweep_start + (sweep_step * nr)
            # set the new voltage to the SMU
            smu.set_voltage(voltage_to_set)
            # get current and voltage from the SMU and append it to the list so we can plot it later
            [current, voltage] = smu.measure_current_and_voltage()
            data_voltage.append(voltage)
            data_current.append(current)
            print(str(voltage)+' V; '+str(current)+' A')
            # Write the data in a csv
            with open(filename_csv, 'a') as csvfile:
                writer = csv.writer(csvfile, delimiter=';',  lineterminator='\n')
                writer.writerow([voltage, current])

        data_current = np.array(data_current)
        data_voltage = np.array(data_voltage)
        indices = np.where(data_current > overall_current_range[cu]/10)
        temperature_for_title = str(temperature[sweep])

        data_current = data_current[indices]
        data_voltage = data_voltage[indices]
        #use plt instead of semilogy to plot in chartesian axis        
        plt.semilogy(data_voltage, np.abs(data_current),'-', linewidth=2)
        # set labels and a title
        plt.xlabel('Voltage / V', fontsize=14)
        plt.ylabel('Current / A', fontsize=14)
        plt.title(f'Characteristic curve of the diode at T =' + temperature_for_title , fontsize=14)
        plt.tick_params(labelsize = 14)
        plt.savefig(filename_pdf)

        # disable the output
        smu.disable_output()
    
#Bring the climate chamber to room temperture so you can safely open it
climate_chamber.go_to_temperature(25, 2, 60)

#disable climate chamber

climate_chamber.disable()



# properly disconnect from the device
sm.disconnect()

""" ******* Plot the Data we obtained ******** """




# set labels and a title
#suggestion: include some more information about the measurement (ref CSV file title)
plt.xlabel('Voltage / V', fontsize=14)
plt.ylabel('Current / A', fontsize=14)
plt.title('Characteristic curve of a diode', fontsize=14)
plt.tick_params(labelsize = 14)



# Connect to eLab 


elab_manager = eLab.Helper_elabftw()
experiment_ID = elab_manager.set_experiment(exp_title)
print(experiment_ID)

# Upload files to eLab
filename_scr = __file__
elab_manager.upload_file(experiment_ID, filename_csv)
elab_manager.upload_file(experiment_ID, filename_pdf)
elab_manager.upload_file(experiment_ID, filename_scr)

#show plot

Used Python code: Powerdiodetemperature.py, measured data: t10all.CSV, t20all.CSV, t30all.CSV and t40all.CSV

Appendix

The following python code is used to fit the double exponential Shockley equation. The files variable path must be adapted to the location where the created data or the downloaded data from this page are stored. Ensure that only usable data files are in the specified folder, as the code will read all files within that directory.

import numpy as np
import csv
import matplotlib.pyplot as plt
from lmfit import Model

# Define the cutter function to filter data
def cutter(x, x_upper_limit, x_lower_limit=0, column=0):
    indices = np.where((x[:, column] < x_upper_limit) & (x[:, column] > x_lower_limit))[0]
    return x[indices, :]

# Define the paths to the CSV files
csv_file_paths = [
    r"C:\Users\obend\OneDrive\Desktop\Studium\SS2024\Semiconductor Lab\Lab1\Python\diode_temp\t10all.CSV",
    r"C:\Users\obend\OneDrive\Desktop\Studium\SS2024\Semiconductor Lab\Lab1\Python\diode_temp\t20all.CSV",
    r"C:\Users\obend\OneDrive\Desktop\Studium\SS2024\Semiconductor Lab\Lab1\Python\diode_temp\t30all.CSV",
    r"C:\Users\obend\OneDrive\Desktop\Studium\SS2024\Semiconductor Lab\Lab1\Python\diode_temp\t40all.CSV"
]

# Initialize a list to store the data arrays
data_arrays = []

# Read each CSV file, convert to a NumPy array, and store in the list
for csv_file_path in csv_file_paths:
    with open(csv_file_path, 'r') as f:
        reader = csv.reader(f, delimiter=';')
        # Skip the header
        next(reader)
        # Read the remaining data
        data = np.array([row for row in reader], dtype=float)
        # Append to the list
        data_arrays.append(data)

# Plot the data from all arrays
plt.figure(figsize=(10, 6))

# Plot each dataset
for i, data_array in enumerate(data_arrays):
    plt.semilogy(data_array[:, 0], data_array[:, 1],'.', label=f'Data (T={(i+1)*10})')

# Add labels and legend
plt.xlabel('Voltage [V]')
plt.ylabel('Current [A]')
plt.legend()
plt.title('Semilogarithmic Plot of Powerdiode characteristic curve at different temperatures')
plt.grid(True, which="both", ls="--")

# Select one dataset for fitting (e.g., T10)
selected_data = data_arrays[0]
selected_data_T20 = data_arrays[1]
selected_data_T30 = data_arrays[2]
selected_data_T40 = data_arrays[3]

V_max_upper = 0.6
V_min_upper = 0.3

V_max_lower = 0.2
V_min_lower = 0

V_max = 0.6
V_min = 0

# Cut the selected data

selected_data_cut_T20 = cutter(selected_data_T20, V_max, V_min)
selected_data_cut_T30 = cutter(selected_data_T30, V_max, V_min)
selected_data_cut_T40 = cutter(selected_data_T40, V_max, V_min)

selected_data_cut = cutter(selected_data, V_max, V_min)
selected_data_cut_T20 = cutter(selected_data_T20, V_max, V_min)
selected_data_cut_T30 = cutter(selected_data_T30, V_max, V_min)
selected_data_cut_T40 = cutter(selected_data_T40, V_max, V_min)

selected_data_cut_l = cutter(selected_data, V_max_lower, V_min_lower)
selected_data_cut_u = cutter(selected_data, V_max_upper, V_min_upper)
# Define the model function
def exponential(V,I_0,T,n):
    kb = 1.38064852e-23
    q = 1.6021766e-19
    T += 273.15
    return I_0 * (np.exp(q * V / (kb * T * n)) - 1)

def double_exponential(V, I_0, n_1, I_1, n_2, T):
    kb = 1.38064852e-23
    q = 1.6021766e-19
    T += 273.15
    return I_0 * (np.exp(q * V / (kb * T * n_1)) - 1) + I_1 * (np.exp(q * V / (kb * T * n_2)) - 1)

# Create a model based on the function
model = Model(double_exponential)
model1 = Model(exponential)

# Create parameters with initial guesses

params_l = model1.make_params(I_0 = 0.1, n = 2, T = 10)
params_u = model1.make_params(I_0 = 0.1, n = 1, T = 10)


# Fix the parameters you want to keep constant

# Perform the fitting using lmfit

result_l = model1.fit(selected_data_cut_l[:,1],params_l,V = selected_data_cut_l[:, 0])
result_u = model1.fit(selected_data_cut_u[:,1],params_u,V = selected_data_cut_u[:,0])

params_init_l = result_l.params
params_init_u = result_u.params


params = model.make_params(I_0=0.09e-10, n_1=1, I_1=10e-9, n_2=1.5, T=10)
params_T20 = model.make_params(I_0=0.1e-10, n_1=1, I_1=0.6e-9, n_2=1.5, T=20)
params_T30 = model.make_params(I_0=0.1e-10, n_1=1, I_1=1.5e-9, n_2=1.5, T=30)
params_T40 = model.make_params(I_0=0.08e-10, n_1=1, I_1=5e-9, n_2=1.5, T=40)

params['I_0'].vary = True
params['T'].vary = False
params['I_1'].vary = True
params['n_1'].vary = False
params['n_2'].vary = False

params_T20['I_0'].vary = True
params_T20['T'].vary = False
params_T20['I_1'].vary = True
params_T20['n_1'].vary = False
params_T20['n_2'].vary = False

params_T30['I_0'].vary = True
params_T30['T'].vary = False
params_T30['I_1'].vary = True
params_T30['n_1'].vary = False
params_T30['n_2'].vary = False

params_T40['I_0'].vary = True
params_T40['T'].vary = False
params_T40['I_1'].vary = True
params_T40['n_1'].vary = False
params_T40['n_2'].vary = False




result = model.fit(selected_data_cut[:, 1], params, V=selected_data_cut[:, 0])
result_T20 = model.fit(selected_data_cut_T20[:, 1], params_T20, V=selected_data_cut_T20[:, 0])
result_T30 = model.fit(selected_data_cut_T30[:, 1], params_T30, V=selected_data_cut_T30[:, 0])
result_T40 = model.fit(selected_data_cut_T40[:, 1], params_T40, V=selected_data_cut_T40[:, 0])
# Print the fitting report
print(result.fit_report())

# Plot the data and the fit


plt.semilogy(selected_data_cut[:, 0], result.best_fit, 'b-', label='fit (T=10)')
plt.semilogy(selected_data_cut_T20[:, 0], result_T20.best_fit, 'y-', label='fit (T=20)')
plt.semilogy(selected_data_cut_T30[:, 0], result_T30.best_fit, 'g-', label='fit (T=30)')
plt.semilogy(selected_data_cut_T40[:, 0], result_T40.best_fit, 'r-', label='fit (T=40)')
plt.xlabel('Voltage [V]')
plt.ylabel('Current [A]')
plt.legend()
plt.show()

# Plot the data and the fits

# Plot the original data
plt.figure(figsize=(10, 6))
plt.semilogy(selected_data_cut[:, 0], selected_data_cut[:, 1], '.', label='data')

# Plot the fit for selected_data_cut (result)
plt.semilogy(selected_data_cut[:, 0], result.best_fit, 'r-', label='fit (T=10)')
plt.title('T10_fit')

plt.figure(figsize=(10, 6))
plt.semilogy(selected_data_cut_T20[:, 0], selected_data_cut_T20[:, 1], '.', label='data')
plt.semilogy(selected_data_cut_T20[:, 0], result_T20.best_fit, 'r-', label='fit (T=20)')
plt.title('T20_fit')
plt.figure(figsize=(10, 6))
plt.semilogy(selected_data_cut_T30[:, 0], selected_data_cut_T30[:, 1], '.', label='data')
plt.semilogy(selected_data_cut_T30[:, 0], result_T30.best_fit, 'r-', label='fit (T=20)')
plt.title('T30_fit')


plt.figure(figsize=(10, 6))
plt.semilogy(selected_data_cut_T40[:, 0], selected_data_cut_T40[:, 1], '.', label='data')
plt.semilogy(selected_data_cut_T40[:, 0], result_T40.best_fit, 'r-', label='fit (T=20)')
plt.title('T40_fit')

# Plot the fit for selected_data_cut_l (result_l)
# plt.semilogy(selected_data_cut_l[:, 0], result_l.best_fit, 'g-', label='fit (T=20)')

# # Plot the fit for selected_data_cut_u (result_u)
# plt.semilogy(selected_data_cut_u[:, 0], result_u.best_fit, 'm-', label='fit (T=30)')

Python code for fitting the double exponential Shockley equation: Fit_all_temps.py

The following python code is used to execute an exponential fit for the region of interest. The files variable path must be adapted to the location where the created data or the downloaded data from this page are stored. Ensure that only usable data files are in the specified folder, as the code will read all files within that directory.

# -*- coding: utf-8 -*-
"""
Created on Mon Jul 29 21:15:27 2024

@author: obend
"""

import numpy as np
import csv
import matplotlib.pyplot as plt
from lmfit import Model

# Define the cutter function to filter data
def cutter(x, x_upper_limit, x_lower_limit=0, column=0):
    indices = np.where((x[:, column] < x_upper_limit) & (x[:, column] > x_lower_limit))[0]
    return x[indices, :]

# Define the paths to the CSV files
csv_file_paths = [
    "t10all.CSV",
    "t20all.CSV",
    "t30all.CSV",
    "t40all.CSV"
]

# Initialize a list to store the data arrays
data_arrays = []

# Read each CSV file, convert to a NumPy array, and store in the list
for csv_file_path in csv_file_paths:
    with open(csv_file_path, 'r') as f:
        reader = csv.reader(f, delimiter=';')
        # Skip the header
        next(reader)
        # Read the remaining data
        data = np.array([row for row in reader], dtype=float)
        # Append to the list
        data_arrays.append(data)

# Plot the data from all arrays
plt.figure(figsize=(10, 6))

# Plot each dataset
for i, data_array in enumerate(data_arrays):
    plt.semilogy(data_array[:, 0], data_array[:, 1],'.',alpha = 0.2, label=f'Data (T={(i+1)*10})')

# Add labels and legend
plt.xlabel('Voltage [V]')
plt.ylabel('Current [A]')
plt.legend()
plt.title('Semilogarithmic Plot of Powerdiode characteristic curve at different temperatures')
plt.grid(True, which="both", ls="--")

# Select one dataset for fitting (e.g., T10)
selected_data = data_arrays[0]
selected_data_T20 = data_arrays[1]
selected_data_T30 = data_arrays[2]
selected_data_T40 = data_arrays[3]

V_max_upper = 0.6
V_min_upper = 0.3

V_max_lower = 0.2
V_min_lower = 0

V_max = 0.07
V_min = 0.01

# Cut the selected data

selected_data_cut_T20 = cutter(selected_data_T20, V_max, V_min)
selected_data_cut_T30 = cutter(selected_data_T30, V_max, V_min)
selected_data_cut_T40 = cutter(selected_data_T40, V_max, V_min)

selected_data_cut = cutter(selected_data, V_max, V_min)
selected_data_cut_T20 = cutter(selected_data_T20, V_max, V_min)
selected_data_cut_T30 = cutter(selected_data_T30, V_max, V_min)
selected_data_cut_T40 = cutter(selected_data_T40, V_max, V_min)

selected_data_cut_l = cutter(selected_data, V_max_lower, V_min_lower)
selected_data_cut_u = cutter(selected_data, V_max_upper, V_min_upper)
# Define the model function
def exponential(V,I_0,T,n):
    kb = 1.38064852e-23
    q = 1.6021766e-19
    T += 273.15
    return I_0 * (np.exp(q * V / (kb * T * n)) - 1)

def double_exponential(V, I_0, n_1, I_1, n_2, T):
    kb = 1.38064852e-23
    q = 1.6021766e-19
    T += 273.15
    return I_0 * (np.exp(q * V / (kb * T * n_1)) - 1) + I_1 * (np.exp(q * V / (kb * T * n_2)) - 1)

# Create a model based on the function
model = Model(exponential)
model1 = Model(exponential)

# Create parameters with initial guesses

params_l = model1.make_params(I_0 = 0.1, n = 2, T = 10) 
params_u = model1.make_params(I_0 = 0.1, n = 1, T = 10)


# Fix the parameters you want to keep constant

# Perform the fitting using lmfit

result_l = model1.fit(selected_data_cut_l[:,1],params_l,V = selected_data_cut_l[:, 0])
result_u = model1.fit(selected_data_cut_u[:,1],params_u,V = selected_data_cut_u[:,0])

params_init_l = result_l.params
params_init_u = result_u.params


params = model.make_params(I_0=1.3e-10, n=1, T=10)
params_T20 = model.make_params(I_0=0.1e-10, n=1, T=20)
params_T30 = model.make_params(I_0=0.1e-10, n=1, T=30)
params_T40 = model.make_params(I_0=0.08e-10, n=1, T=40)

params['I_0'].vary = True
params['T'].vary =  False

params['n'].vary = True


params_T20['I_0'].vary = True
params_T20['T'].vary = False

params_T20['n'].vary = True


params_T30['I_0'].vary = True
params_T30['T'].vary = False

params_T30['n'].vary = True


params_T40['I_0'].vary = True
params_T40['T'].vary = False

params_T40['n'].vary = True





result = model.fit(selected_data_cut[:, 1], params, V=selected_data_cut[:, 0])
result_T20 = model.fit(selected_data_cut_T20[:, 1], params_T20, V=selected_data_cut_T20[:, 0])
result_T30 = model.fit(selected_data_cut_T30[:, 1], params_T30, V=selected_data_cut_T30[:, 0])
result_T40 = model.fit(selected_data_cut_T40[:, 1], params_T40, V=selected_data_cut_T40[:, 0])
# Print the fitting report
print('T10..................................................................................')
print(result.fit_report())
print('T20..................................................................................')
print(result_T20.fit_report())
print('T30..................................................................................')
print(result_T30.fit_report())
print('T40..................................................................................')
print(result_T40.fit_report())
# Plot the data and the fit


plt.semilogy(selected_data_cut[:, 0], result.best_fit, 'b-', label='fit (T=10)')
plt.semilogy(selected_data_cut_T20[:, 0], result_T20.best_fit, 'y-', label='fit (T=20)')
plt.semilogy(selected_data_cut_T30[:, 0], result_T30.best_fit, 'g-', label='fit (T=30)')
plt.semilogy(selected_data_cut_T40[:, 0], result_T40.best_fit, 'r-', label='fit (T=40)')
plt.xlabel('Voltage [V]')
plt.ylabel('Current [A]')
plt.legend()
plt.show()

# Plot the data and the fits

# plt.figure(figsize=(10, 6))
# plt.semilogy(selected_data_cut[:, 0], selected_data_cut[:, 1], '.',alpha= 0, label='data')


# plt.semilogy(selected_data_cut[:, 0], result.best_fit, 'r-', label='fit (T=10)')
# plt.title('T10_fit')

# plt.figure(figsize=(10, 6))
# plt.semilogy(selected_data_cut_T20[:, 0], selected_data_cut_T20[:, 1], '.',alpha = 0.2, label='data')
# plt.semilogy(selected_data_cut_T20[:, 0], result_T20.best_fit, 'r-', label='fit (T=20)')
# plt.title('T20_fit')
# plt.figure(figsize=(10, 6))
# plt.semilogy(selected_data_cut_T30[:, 0], selected_data_cut_T30[:, 1], '.',alpha = 0.2, label='data')
# plt.semilogy(selected_data_cut_T30[:, 0], result_T30.best_fit, 'r-', label='fit (T=20)')
# plt.title('T30_fit')


# plt.figure(figsize=(10, 6))
# plt.semilogy(selected_data_cut_T40[:, 0], selected_data_cut_T40[:, 1], '.', alpha = 0.2,label='data')
# plt.semilogy(selected_data_cut_T40[:, 0], result_T40.best_fit, 'r-', label='fit (T=20)')
# plt.title('T40_fit')

# Plot the fit for selected_data_cut_l (result_l)
# plt.semilogy(selected_data_cut_l[:, 0], result_l.best_fit, 'g-', label='fit (T=20)')

# # Plot the fit for selected_data_cut_u (result_u)
# plt.semilogy(selected_data_cut_u[:, 0], result_u.best_fit, 'm-', label='fit (T=30)')

Python code for systematical fitting of regions of interest: Fit_all_temps_exponential.py

Temperature-Dependent Current-Voltage Characteristics of a Power Diode

Course: Research Laboratory Semiconductor Devices (PHT.311UF)
Group S4: Felix Obendorf & Fabian Macher
Period: Summer 2024
Instructor: Karin Zojer & Peter Hadley

Introduction

Determining the non-ideality factor n

Fitting the characteristic curve with a modified Shockley Equation

Appendix