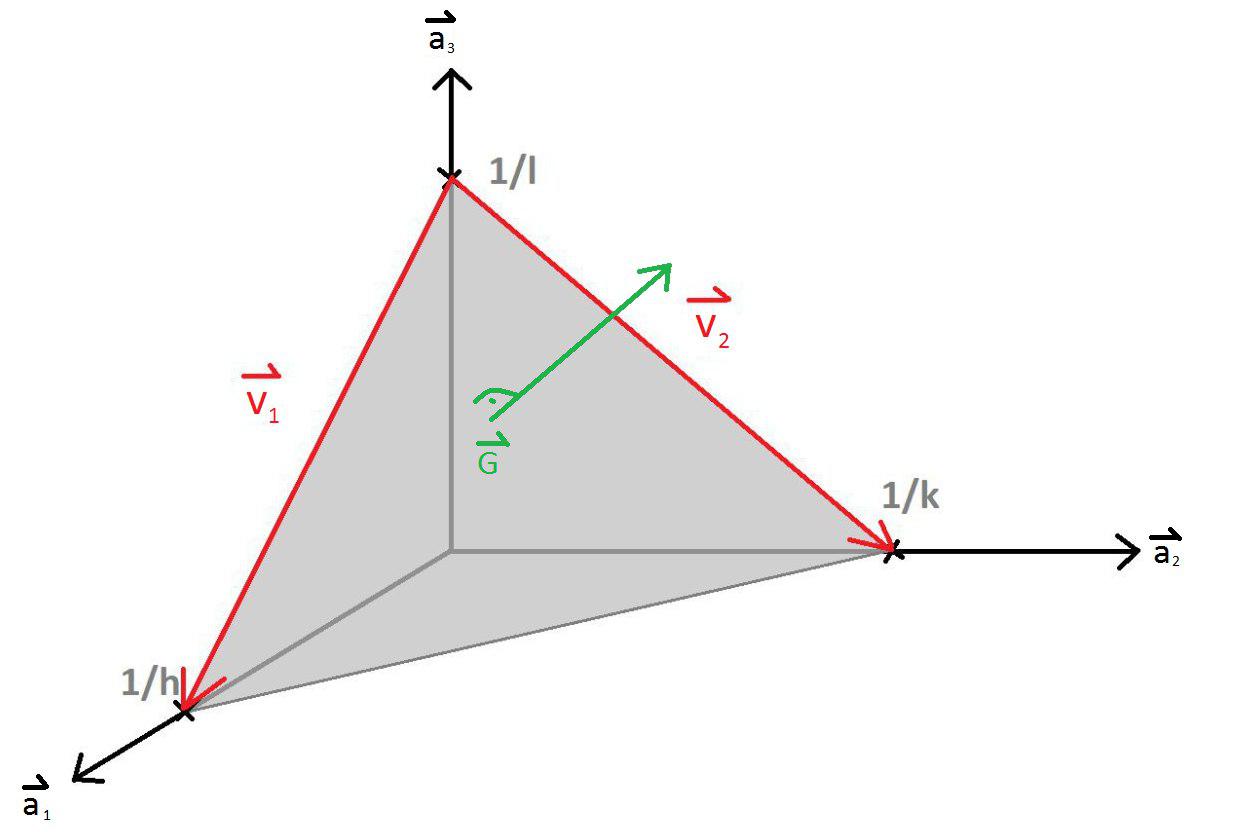
The $(hkl)$ plane intercepts the axis in the direction of $\vec{a}_1$ at $\frac{|\vec{a}_1|}{h}$, the axis in the direction of $\vec{a}_2$ at $\frac{|\vec{a}_2|}{k}$, and the axis in the direction of $\vec{a}_3$ at $\frac{|\vec{a}_3|}{l}$. The three points that define the $(hkl)$ plane are $\left( \frac{a_{1x}}{h},\frac{a_{1y}}{h},\frac{a_{1z}}{h} \right)$, $\left(\frac{a_{2x}}{k},\frac{a_{2y}}{k},\frac{a_{2z}}{k} \right)$, and $\left(\frac{a_{3x}}{l},\frac{a_{3y}}{l},\frac{a_{3z}}{l}\right)$. The normal vector to this plane can be determined by taking the cross product of two vectors in the plane. Two suitable vectors are $\vec{v}_1=\frac{\vec{a}_1}{h}-\frac{\vec{a}_3}{l}$ and $\vec{v}_2=\frac{\vec{a}_2}{k}-\frac{\vec{a}_3}{l}$.

Every lattice has a reciprocal lattice where the reciprocal lattice vectors can be written in term of primitive lattice vectors in reciprocal space,
\[ \begin{equation} \vec{G}_{hkl}=h\vec{b}_1+k\vec{b}_2+l\vec{b}_3. \end{equation} \]The reciprocal lattice vector $\vec{G}_{hkl}$ can be shown to be normal to the $(hkl)$ plane by taking the inner product of $\vec{G}_{hkl}$ with both $\vec{v}_1$ and $\vec{v}_2$. Since both of these inner products are zero, $\vec{G}_{hkl}$ is normal to $(hkl)$.
\[ \begin{equation} \vec{v}_1\cdot\vec{G}_{hkl}=\left(\frac{1}{h}{h}\vec{b}_1 \cdot \vec{a}_1-\frac{1}{l}{l}\vec{a}_3 \cdot \vec{b}_3\right)= 2\pi - 2\pi = 0 \end{equation} \] \[ \begin{equation} \vec{v}_2\cdot\vec{G}_{hkl}=\left(\frac{1}{k}{k}\vec{a}_2 \cdot \vec{b}_2-\frac{1}{l}{l}\vec{b}_3 \cdot \vec{a}_3\right)= 2\pi - 2\pi = 0 \end{equation} \]Here we used the fact that the inner product of the primitive lattice vectors in real space and the primitive latice vectors in reciprocal space satisfy,
$$\vec{a}_i\cdot\vec{b}_j=2\pi\delta_{ij},$$where $\delta_{ij}$ is the Kronecker delta.