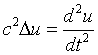
Derivations for the Photon Wave Equation table

Go back to the Photon Wave Equation table.

The Wave Equation and it's Solutions

We'll start out with the wave equation in n dimensions

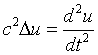
with the speed of light c, the laplace operator Δ, the photon wave function u and the time t.

The solutions of the wave equation are

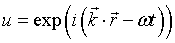
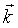where i is the imaginary unit, the wave vector, 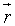the position vector in real space and ω the wave frequency.

This is easily proven, as the second time derivative of u yields

and the left side of the wave equation turns out to be
The wave equation is fulfilled for
which is the dispersion relation for n dimensions.

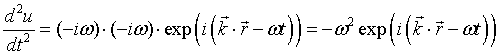
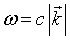
In real space, the solutions u are harmonic waves with the frequency ω, travelling along the direction of 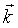with the wavelength

and the energy
with the reduced Planck constant .

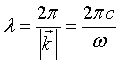
In reciprocal space (k-space), these solutions represent only points (i.e. states) with the position .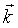

Density of States

Given a n-dimensional box in real space with a sidelength of L and a volume of

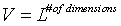
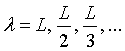
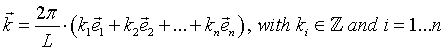
we can try to fit in as many waves as possible. Taking into account periodic boundary conditions, we end up with possible values for the wavelength of
which results in possible wave vectors
where the s are unitary basis vectors in k-space. So the k-space only contains equally spaced states in a cubical lattice with a distance between two neighbours of 2π / L. This means, the 1st Brillouin zone has a volume of

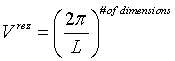
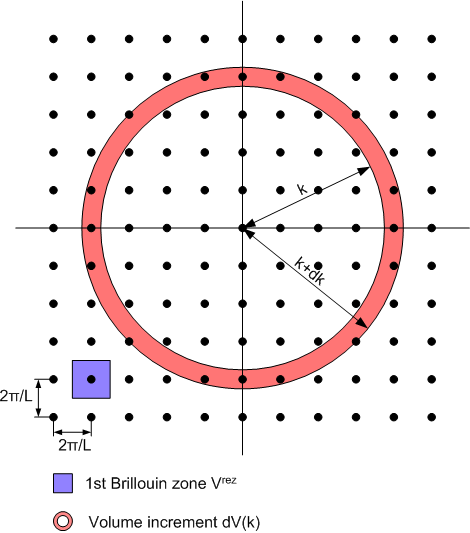
Example of a twodimensional k-space. Drawn in are several states (black points), the first Brilloin zone of one state (blue rectangle) and the volume increment dV(k) (red annulus circular ring).

The numbers of states having a wave number between k and k+dk are given by the numbers of possible polarisations p times the volume increment dV(k) in k-space divided by the space one state occupies, i.e. Vrez. The volume increment dV(k) itself is determined by the area Arez of the surface with given k times dk.

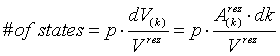
This leads immediatly to the density of states, which is defined as the numbers of states divided by the volume of our n-dimensional box in real space and wave number increment dk.

Of course, the density of states can also be expressed with respect to the frequency ω, the wavelength λ or the energy E:

Internal Energy

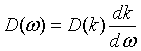
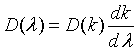
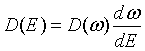
The distribution of the internal energy u(λ) is easily obtained by multiplying the energy with the density of states and the probability that a photon will have the specified energy. The last factor is known as the Bose-Einstein distribution.

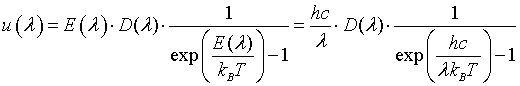
The internal energy U of our n-dimensional box can be determined by integrating it's distribution u(λ) from zero to infinity and multiplying it with the volume of the box V.

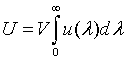
If you insert the energy distribution and try to evaluate the expression for the internal energy, following definite integral will most likely appear:

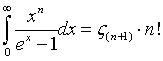
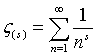
for n > 0, with the Riemann Zeta function

The other thermodynamic properties (specific heat cV, entropy S, free energy F and the pressure P) are easily obtained by their definitions, which are given in the table Results of the Photon Wave Equation in n dimensions.

Black Body Radiation

For the derivation of the black body radiation, we have to imagine a n-dimensional hemisperical container, with a constant internal energy distribution u(λ) inside and a small hole dA cut into the center of it's face. The vector pointing out of this small hole is .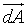

The intensity distribution of the black body radiation is the amount of energy flow I(λ) coming out of this hole. The energy flow from the solid angle element dΩ can be expressed as the energy dE(&lambda, &Omega) passing the hole in the time interval between t and t + dt, divided by the length of the interval dt.

Let's analyse the volume dV, which gets passed through the hole in the time interval described above. Because the photons are moving isotropic inside our container, only the fraction dΩ divided by the total solid angle ΩR, of the photons inside the volume dV will pass the hole. The energy, all the photons inside the volume will carry through the hole is therefore given as

When expressing the volume dV by the vector product of a length and the area vector 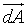and plugging this into the formula for the energy flow, we find the photon's velocity vector

While the magnitude of the velocity vector must be the speed of light c, it's direction can be expressed by the unitary vector 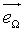pointing into the direction Ω. Altogether, this yields for the energy flow from the solid angle element dΩ

Integrating over the solid angle ΩR/2 of our hemisphere, we obtain for the intensity distribution of the black body radiation

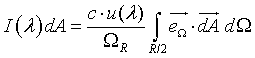
The Wien's Law is easily calculated for a given radiation distribution. It expresses the wavelength of the intensity maximum λmax as a function of the temperature T. Just zero in the first derivative of the radiation intensity I(λ) with respect to the wavelength.

Also the Stefan-Boltzmann Law can be derived quite easily from the radiation distribution. It is just the integral of the distribution I(λ) from wavlength λ = 0 to infinity.

Go back to the Photon Wave Equation table.