Density of states → energy spectral density for electrons in metals

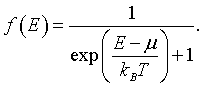
Fermions obey Fermi-Dirac statistics. The probablility that a fermion state at energy E is occupied is given by the Fermi function,

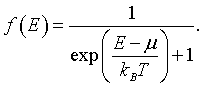
Here μ is the chemical potential. The energy spectral density u(E) is the energy times the density of states D(E) times the Fermi function.

The form below calculates the energy spectral density numerically from the density of states. The density of states is input as two columns of text in the textbox below. The first column is the energy in eV. The second column is the density of states in unit of eV^-1 m^-d, where d is the dimensionality (1,2, or 3). The electron density can be calculated from the number of electrons per unit cell and the volume of the unit cell or it can be input directly. After the 'DoS → u(E)' button is pressed, the density of states is plotted on the left and u(E) is plotted on the right. The data for the u(E) plot also appear as six columns of text in the lower right textbox. The first column is the energy in eV. Columns 2-6 are the energy spectral density u(E) for five temperatures 0.2T_max, 0.4T_max...T_max in units are m^-d.