Density of states → Helmholtz free energy density f(T)

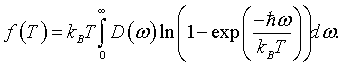
Using statistical mechanics, it can be shown that the Helmholtz free energy density f(T) for bosons can be expressed as the following integral,

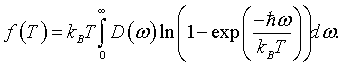
Here $\hbar\omega$ is the energy of phonons with frequency ω and D(ω) is the density of states. This result is discussed in Statistical Physics, Part 1 by Landau and Lifshitz and in the notes on the thermodynamic properties of non-interacting bosons.

The form below uses this formula to calculate the temperature dependence of the Helmholtz free energy density from tabulated data for the density of states. The density of states data is input as two columns in the textbox at the lower left. The first column is the angular-frequency ω in rad/s. The second column is the density of states in units of s rad^-1m^-3.

After the 'DoS → f(T)' button is pressed, the density of states is plotted on the left and f(T) is plotted from temperature T_min to temperature T_max on the right. The data for the f(T) plot also appears in tabular form in the lower right textbox. The first column is the temperature in Kelvin and the second column is the Helmholtz free energy density in units of J m^-3.

Load a phonon density of states: 
Nearest-neighbor mass-spring models: