Two dimensional Wigner-Seitz cell
In three-dimensions, there are 14 possible Bravais lattices.
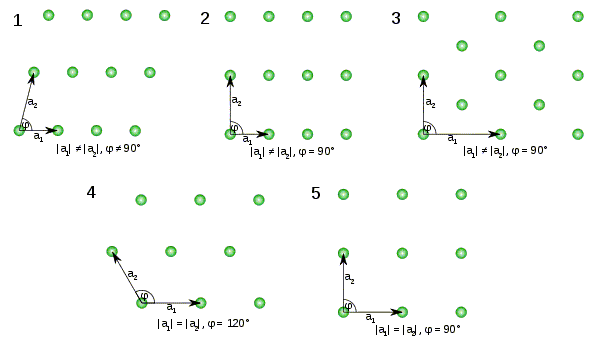
In two-dimensions, there are only five possible Bravais lattices:
- Oblique lattice with a ≠ b and γ ≠ 90° (γ is the angle between the vectors a and b, a = |a|, and b = |b|)
- Rectangular lattice with a ≠ b and γ = 90°
- Face centered rectangular lattice with a ≠ b and γ = 90°
- Hexagonal lattice with a = b and γ = 120°
- Square lattice with a = b and γ = 90°
Construct the two-dimensional Wigner-Seitz cell for
a) an oblique lattice with a = 5 Å , b = 4.4 Å and γ = 63°
b) a face centered rectangular lattice with a = 4 Å and b = 8 Å
c) a rectangular lattice with a = 6 Å and b = 8 Å.
determine also
- the area of the conventional (crystallographic) unit cell
- the area of the Wigner-Seitz cell
- the translational vectors which construct the lattice from the Wigner-Seitz cells.
|