First name
Last name
Matrikelnr.
Problem 1
Methanol consists of one carbon atom, one oxygen atom, and four hydrogen atoms.

(a) What is the molecular orbital Hamiltonian for methanol?
(b) Carbon atoms have six protons and oxygen atoms have eight protons. How many molecular orbitals would be occupied in the ground state of methanol?
(c) What kind of bond is the C-O bond? How could you calculate the bond potential of this bond?
(d) How many translational, vibrational, and rotational modes does methanol have?
Problem 2
A diffraction experiment is performed on a single crystal of Ni using X-rays with a wavelength of 1.54 Å. The netplanes are indexed using the unit vectors of the conventional unit cell. This means that even though Ni is fcc, it is considered to be simple cubic with four atoms in the basis. The Bragg angle of the (220) reflection is 38.2°.
(a) What is the length of the $\vec{G}_{220}$ reciprocal lattice vector in terms of the lattice constant $a$?
(b) What is the diffraction condition that relates the X-ray wavenumber to the reciprocal lattice vector $\vec{G}_{220}$.
(c) Determine the lattice constant $a$.
Problem 3
Silicon has an fcc Bravais lattice. There are two atoms in the basis.
(a) Sketch approximately the phonon dispersion relation for diamond along $L-\Gamma -X$. $\overline{\Gamma L} = \frac{\sqrt{3}\pi}{a},\quad\overline{\Gamma X} = \frac{2\pi}{a}$.
(b) What is the form of the normal mode solutions for silicon?
(c) How many transverse normal modes are there for a crystal with $N$ atoms?
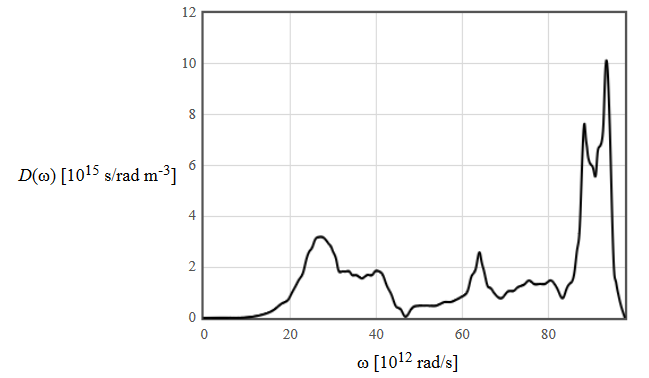
(d) The phonon density of states for silicon is shown below. Which of these states would be occupied at 300 K?
Problem 4
(a) Using the empty lattice approximation, draw the electronic band structure of a bcc metal.

(b) This metal has two valence electrons per unit cell. Include the Fermi energy in your drawing.
(c) $E=0$ is indicated in the plot. What is approximately the Fermi energy in electron volts if the lattice constant is $a=4.3$ Å?
(d) What experimental techniques can be used to measure the electron density of states?
Quantity | Symbol | Value | Units | |
| electron charge | e | 1.60217733 × 10-19 | C | |
| Planck's constant | h | 6.6260755 × 10-34 | J s | |
| Boltzmann's constant | kB | 1.380658 × 10-23 | J/K | |
| electron mass | me | 9.1093897 × 10-31 | kg | |
| speed of light | c | 2.99792458 × 108 | m/s |