Problem 1
At very low temperatures, He₂ molecules will form. A helium atom has two protons and two electrons. These molecules are held together by Van Der Waals forces.

(a) Write down the molecular orbital Hamiltonian that needs to be solved to find the molecular orbitals.

(b) What linear combination of atomic orbitals would you guess would be a good solution to the molecular orbital Hamiltonian?

(c) If the molecular orbitals are called $\phi_{\text{mo1}},\,\phi_{\text{mo2}},\,\phi_{\text{mo2}},\,\cdots$; what is the many-electron ground-state wavefunction for a He₂ molecule?

Problem 2
Gold has an fcc crystal structure. Suppose you have a table of the atomic form factor of gold and you want to calculate the ratio of the squares of the structure factors for the 111 and 300 reflections,

Describe how you could perform this calculation.

Problem 3
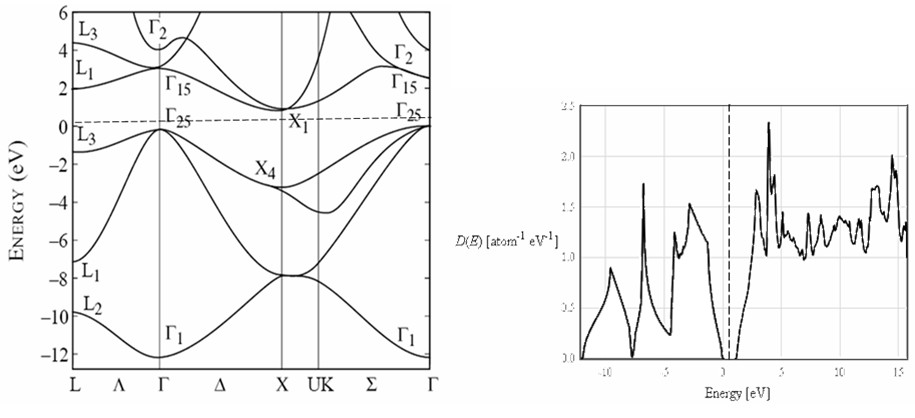
The electronic band structure and corresponding density of states for a material is shown below. The Fermi energy is indicated by the dotted line.

(a) Is this a material a good thermal conductor? Why or why not?

(b) How would you compute the electronic component of the specific heat from this data? Sketch the approximate form of the specific heat as a function of temperature.

Problem 4
A polymer can be considered to be a one dimensional crystal where the monomer is the unit cell. Draw approximately the electron dispersion ($E$ vs. $k$) for a polymer. Most monomers have an even number of electrons. This is because molecules with an odd number of electrons are radicals and are chemically unstable. If there are an even number of electrons in the unit cell, is this a metal or an insulator? Explain your reasoning.