First name
Last name
Matrikelnr.
Problem 1
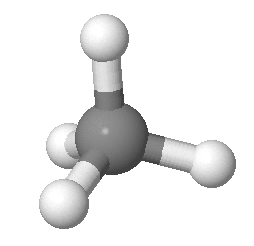
Methane consists of one carbon atom and four hydrogen atoms.

(a) What is the molecular orbital Hamiltonian for methane?
(b) Both the sp³ hybrid orbitals and the molecular orbitals of methane can be expressed as a linear combination of atomic orbitals. What is the difference between the sp³ orbitals and the molecular orbitals of methane?
(c) How many molecular orbitals are filled in the ground state of methane?
(d) Are the C-H bonds σ-bonds or π-bonds? Why?
(e) How many translational, vibrational, and rotational modes does methane have?
First name
Last name
Matrikelnr.
Problem 2
A primitive unit cell and lattice parameters of hexagonal boron nitride (3D h-BN) are shown in two orientations.
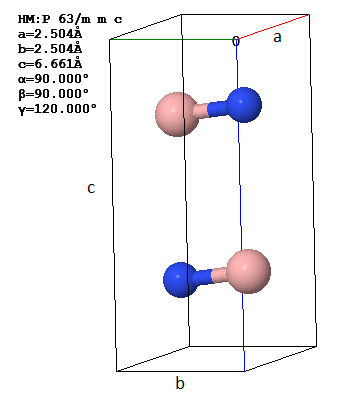
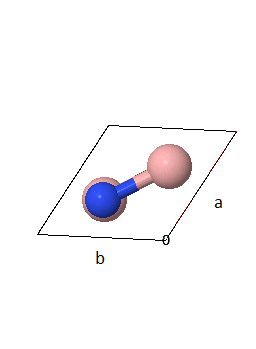
(a) How many atoms are there in the asymmetric unit?
(b) Does 3D h-BN have inversion symmetry? How can you tell?
(c) Draw the (001) plane indicating the boron atoms with open circles and the nitrogen atoms with filled circles. Your drawing should include at least four primitive unit cells.
(d) The number of diffraction peaks that can be observed in a diffraction experiment can be determined using the Ewald sphere. The shorter the wavelength, the more diffraction peaks are observed. What is the maximum wavelength where at least one diffraction peak will be observed for 3D h-BN?
The first Brillouin zone of 3D h-BN is,
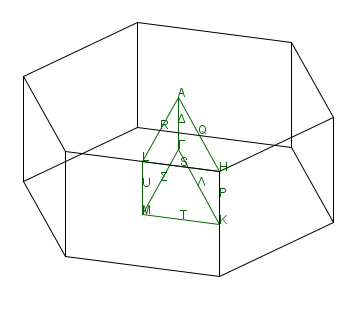
(e) Sketch the phonon dispersion of 3D h-BN along $A-\Gamma -K - M$.
(f) 3D h-BN is an insulator with a direct band gap in the ultraviolet region. Sketch the electronic dispersion relation ($E$ vs $k$) along $A-\Gamma -K - M$. Include the chemical potential in your drawing.
(g) Describe how the electronic dispersion relation ($E$ vs $k$) of 3D h-BN could be calculated using the tight-binding method.
(h) If the dispersion relation of ($E$ vs $k$) is known, how could the chemical potential be calculated?
Problem 3
(a) What is the Sommerfeld expansion?
(b) Why can the Sommerfeld expansion not be used to describe the thermodynamic properties of insulators?
(c) What is the Wiedemann–Franz law?
(d) The chemical potential of a metal is weakly temperature dependent so it can be estimated by calculating the Fermi energy. A monovalent metal has a simple cubic lattice and a lattice constant of $a= 0.1$ nm. Use the free electron model to estimate the chemical potential in this case.
Quantity | Symbol | Value | Units | |
| electron charge | e | 1.60217733 × 10-19 | C | |
| speed of light | c | 2.99792458 × 108 | m/s | |
| Planck's constant | h | 6.6260755 × 10-34 | J s | |
| reduced Planck's constant | $\hbar$ | 1.05457266 × 10-34 | J s | |
| Boltzmann's constant | kB | 1.380658 × 10-23 | J/K | |
| electron mass | me | 9.1093897 × 10-31 | kg | |
| Stefan-Boltzmann constant | σ | 5.67051 × 10-8 | W m-2 K-4 | |
| Bohr radius | a0 | 0.529177249 × 10-10 | m | |
| atomic mass constant | mu | 1.6605402 × 10-27 | kg | |
| permeability of vacuum | μ0 | 4π × 10-7 | N A-2 | |
| permittivity of vacuum | ε0 | 8.854187817 × 10-12 | F m-1 | |
| Avogado's constant | NA | 6.0221367 × 1023 | mol-1 |