Problem 1
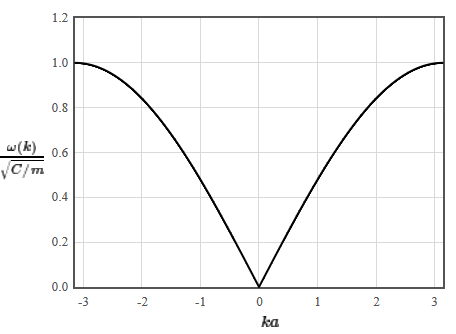
Consider a one-dimensional crystal with a macroscopic dimension of $4$ cm and a lattice constant of $a = 0.3$ nm. Locate the origin of the reciprocal lattice in the center of the Brillouin cell. Consider only longitudinal phonon modes with a dispersion relation $\omega (k)$ with the spring constant $C = 170$ N/m and a mass $m = 1.5 \times 10^{-26}$ kg. The dispersion relation is,

a) What is the number $(N)$ of possible wave vectors $k$ for phonon states within the first Brillouin zone?

b) Determine the sound velocity $(v)$.

c) What is the largest possible energy $(E)$ which a phonon can take?

d) Write down the normal mode function of a phonon ($u_s$, with $s$ as the index of the individual atoms) with the largest wavevector $k$ of the system. Explain the quantities you use for the function.

- useful fundamental parameters could be: $\hbar = 1.05 \times 10^{-34}$ Js.

Problem 2
Consider a monovalent metal in a simple cubic lattice (lattice constant $a = 0.3$ nm) with one atom per unit cell. The origin of the reciprocal lattice is located in the center of the first Brillouin cell. The crystal has the shape of a cube with side length $L = 1$ cm. The density of states $D(k)$ is given below.

The system has a Fermi energy $E_F$ of $6.47 \times 10^{-19}$ J = $4.04$ eV.

a) Write down the general wavefunction $\psi$ of the electronic state with the wavevector $k$ in the free electron model. Write down the periodic boundary condition for the three-dimensional case.

b) Determine the density of states as a function of energy $D(E)$.

c) What is the probability that the electronic state at the energy $E = \mu$ (with $\mu$ as the chemical potential) is occupied?

d) Does the Fermi surface intersect with the Brillouin zone boundary? Why or why not?

- useful fundamental parameters could be: $m_e = 9.11\times 10^{-31}$ kg and $\hbar = 1.05 \times 10^{-34}$ Js.

Problem 3
The orthorhombic point group 222 is generated by two-fold rotation axes (rotation around 180°), two of these rotation axes (one around the $x$-axis and one around the $z$-axis) are required to span this group.

a) Write down the two generating matrices for this point group.

b) Give all symmetry elements of this point group.

c) Does this group has an inversion center? Why or why not?

d) Give definition for Gibbs free energy $(G)$ where the independent variables are the temperature $T$, the electric field $(E)$, the magnetic field $(H)$ and the external stress $(\sigma )$. Give the physical quantities of the different symbols used, please use tensor notation.