First name
Last name
Matrikelnr.
Problem 1
In the ground state of a hydrogen molecule H2, both electrons are in the lowest molecular orbital and have opposite spin.
(a) How do the two electrons occupy the molecular orbitals in the first excited state of H2 and what are the possibilities for the spins?
(b) The first excited state splits in a spin singlet and a spin triplet. Explain what the singlet and triplet states are.
1. (c) What is the energy difference between the singlet and triplet states and how is this energy calculated?
First name
Last name
Matrikelnr.
Problem 2
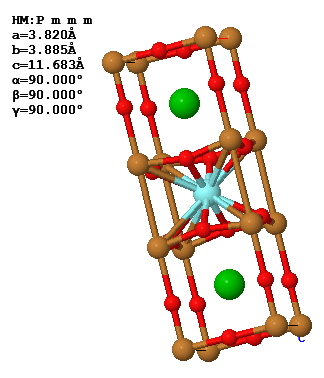
The conventional unit cell and the lattice parameters of the superconductor YBa2Cu3O7 is shown below.

(a) What is the Bravais lattice of YBa2Cu3O7?
(b) What are the primitive lattice vectors in reciprocal space?
$\vec{b}_1=$
$\vec{b}_2=$
$\vec{b}_3=$
(c) Could YBa2Cu3O7 be piezoelectric? Why or why not?
(d) Sketch the phonon dispersion relation of YBa2Cu3O7 along $X - \Gamma - R$. The distances to the Brillouin zone boundaries are,
\begin{equation} \overline{\Gamma X}=\frac{\pi}{a},\,\overline{\Gamma R} = \pi\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}\approx 1.44\frac{\pi}{a}. \end{equation}(e) Above the superconducting transistion temperture YBa2Cu3O7 is a low electron density metal. How does the specific heat of YBa2Cu3O7 compare to a good metal like silver?
Problem 3
(a) Draw approximately the electron dispersion relation and the density of states for the one-dimensional potential, $V(x) = \cos\left(\frac{2\pi x}{a}\right)$ eV.
(b) There are 3 electrons per primitive unit cell, draw the position of the chemical potential in the plots of the dispersion relation and the density of states.
(c) Is this material a metal, a semiconductor, or an insulator? Why?
Problem 4
Tight binding is a method to calculate the electronic band structure of a crystal. The tight-binding wavefunction is,
\begin{equation} \psi_{\vec{k}}\left(\vec{r}\right)=\frac{1}{\sqrt{N}}\sum\limits_{h,j,l}e^{i\left(h\vec{k}\cdot\vec{a}_1 + j\vec{k}\cdot\vec{a}_2 + l\vec{k}\cdot\vec{a}_3\right)} \psi_{\text{unit cell}}\left(\vec{r}-h\vec{a}_1-j\vec{a}_2-l\vec{a}_3\right). \end{equation}Here $N$ is the number of unit cells in the crystal; $h$, $j$, and $l$ are integers that are used to label all the unit cells in the crystal; $\vec{k}$ is a wave vector; $\vec{a}_1$, $\vec{a}_2$, and $\vec{a}_3$ are primitive lattice vectors in real space, and $\psi_{\text{unit cell}}(\vec{r})$ is a trial wavefunction that is constructed from the valence orbitals $\phi_{i}$ of all of the atoms in a primitive unit cell,
\begin{equation} \psi_{\text{unit cell}}\left(\vec{r}\right)=\sum\limits_{i}c_{i}\phi_{i}\left(\vec{r}-\vec{r}_i\right). \end{equation}Sodium has a bcc Bravais lattice and the valence orbitals are the 3s atomic orbitals.
(a) What is $\psi_{\text{unit cell}}$ for sodium? How many coefficients $c_i$ are there?
(b) How do you determine the coefficients $c_i$ for sodium?
(c) If the coefficients $c_i$ are known, how can you construct the dispersion relation for sodium?
(d) If the dispersion relation for sodium is known, how can you construct the density of states? Sketch approximately the electron density of states for sodium.
(e) If the density of states for sodium is known, how can you calculate the chemical potential? Describe how this calculation depends on the number of valence orbitals that are included in the tightbinding calculation.
Quantity | Symbol | Value | Units | |
| electron charge | e | 1.60217733 × 10-19 | C | |
| speed of light | c | 2.99792458 × 108 | m/s | |
| Planck's constant | h | 6.6260755 × 10-34 | J s | |
| reduced Planck's constant | $\hbar$ | 1.05457266 × 10-34 | J s | |
| Boltzmann's constant | kB | 1.380658 × 10-23 | J/K | |
| electron mass | me | 9.1093897 × 10-31 | kg | |
| Stefan-Boltzmann constant | σ | 5.67051 × 10-8 | W m-2 K-4 | |
| Bohr radius | a0 | 0.529177249 × 10-10 | m | |
| atomic mass constant | mu | 1.6605402 × 10-27 | kg | |
| permeability of vacuum | μ0 | 4π × 10-7 | N A-2 | |
| permittivity of vacuum | ε0 | 8.854187817 × 10-12 | F m-1 | |
| Avogado's constant | NA | 6.0221367 × 1023 | mol-1 |