Problem 1
Consider a molecule formed by a helium atom and a hydrogen atom. The helium atom consists of two protons (and two neutrons) in the atomic nucleus (mass $m_{\alpha}$ at position $\vec{r}_{\alpha}$) paired with two electrons (mass $m_e$ at positions $\vec{r}_1$ and $\vec{r}_2$) both in the 1s state. The hydrogen atom has one proton in its atomic nucleus (mass $m_p$ at position $\vec{r}_p$) paired with one electron (mass $m_e$ at position $\vec{r}_3$) in the 1s shell.

a) The first question is related to the many particle Hamiltonian for the molecule HeH. Write down all parts where the single electron of hydrogen is involved. Please use the proper masses ($m_{\alpha}$, $m_{p}$, $m_{e}$), their charges ($\pm e$, $+2e$) and their positions ($\vec{r}_{\alpha}$, $\vec{r}_p$, $\vec{r}_1$, $\vec{r}_2$, $\vec{r}_3$) of the involved particles.

b) Write down the molecular orbital Hamiltonian for a single electron for the molecule HeH. How many terms does this Hamiltonian consists of?

c) A molecular orbital wavefunction (MO-wavefunction) can be constructed by a linear combination of atomic orbitals. Write down the Ansatz for the MO-wavefunction using atomic orbitals.

d) Solving the Roothan equations reveal molecular orbital wavefunctions and their respective energies. How many MO wavefunctions (and energy levels) are obtained? How many energy levels are occupied by the electrons?

Problem 2
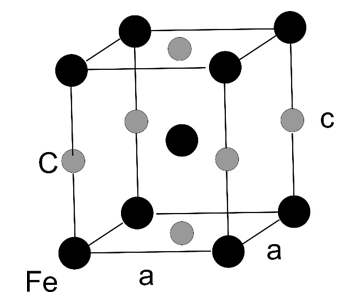
Martensite is an iron-carbon alloy which crystallizes in a tetragonal structure ($a_1 = a_2 = a$, $a_3 = c$, $\alpha = \beta = \gamma =$ 90°). A sketch of the crystallographic unit cell is given below with the black spheres are iron atoms and the light grey spheres are carbon atoms.

a) Write down a set of conventional lattice vectors $\vec{a}_1,\, \vec{a}_2,$ and $\vec{a}_3$.

b) Calculate the mass density of the crystal structure. The lattice constants are $a = 2.842 \times 10^{-10}$ m, $c = 3.008 \times 10^{-10}$ m, and the atomic weight for one mol for iron and carbon is 55.85 g and 12.01 g, respectively.

c) What is the Bravais lattice type? Please note that there exists two different Bravais lattice types for the tetragonal system: body centred tetragonal and primitive tetragonal.

d) Give the basis of the crystal structure in fractional coordinates of the lattice vectors $\vec{a}_1,\, \vec{a}_2,$ and $\vec{a}_3$.

Problem 3
An orthorhombic 3-dimensional reciprocal lattice is given with lattice constants $b_1 = 6$ Å^-1, $b_2 = 3$ Å^-1, and $b_3 = 4$ Å^-1 (see below).

a) Give the volume of the first Brillouin zone ( the Wigner Seitz cell of the reciprocal lattice).

b) Diffraction should be observed of the 120 reflection. Draw wave vectors of the incident beam (with symbol $\vec{k}$) and of the scattered beam (with symbol $\vec{k}'$) for observation of the 120 diffraction peak. The wavelength of the primary beam can be chosen freely.

c) Calculate the scattering angle $2\theta$ for the diffraction peak 120 if the wavelength of the incident beam is 1 Å. Please note that the angle $2\theta$ encloses the angle between the vectors $\vec{k}$ and $\vec{k}'$.

d) Determine quantities of the real lattice: the length and direction of the lattice constants $a_1$ and $a_2$.