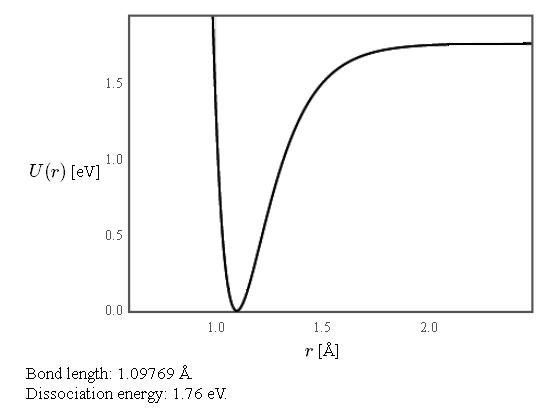
513.001 Molecular and Solid State Physics
9.5.2014

Problem 1
The Morse potential for a N₂ molecule is shown below.

(a) How can this bond potential be calculated?

(b) How can this information be used to calculate the frequencies of light that will be absorbed by an N₂ molecule? Consider the electronic, vibrational, and rotational energy levels.

Solution

The energy of the bond potential of a N2 molecule can be calculated with the equation,

\[ \begin{equation}
E = \frac{\langle \psi|H_{elec}|\psi \rangle }{\langle\psi|\psi\rangle}
\end{equation} \].

Where the electronic Hamiltonian is given by,

\[ \begin{equation}
H_{elec} = -\sum_{i=1}^{14} \frac{\hbar^2}{2m}\vec{\nabla}_i^2-
\sum_{i=1}^{14}\frac{Z_1e^2}{4\pi\epsilon_0|\vec{r}_i - \vec{R}_1|}-\sum_{i=1}^{14}\frac{Z_2e^2}{4\pi\epsilon_0|\vec{r}_i - \vec{R}_2|} \\
+ \sum_{i < j}^{14} \frac{e^2}{4\pi\epsilon_0|\vec{r}_i-\vec{r}_j|}
+ \frac{Z_1Z_2e^2}{4\pi\epsilon_0|\vec{R}_1-\vec{R}_2|}
\end{equation} \]

where $Z_1 = Z_2 = 7 $ is the nuclear charge.

To determine the ground state wavefunction, fix the positions of the nuclei by choosing values for $\vec{R}_1$ and $\vec{R}_2$ and <a href="http://lampz.tugraz.at/~hadley/ss1/molecules/mo.php">solve for the molecular orbitals</a> using LCAO. Then use a Slater determinant to construct the ground state many-electron wavefunction $\psi(\vec{r}_1, \cdots, \vec{r}_{14}) $. For the ground state, use the seven molecular orbitals with the lowest energies and include them each in the Slater determinant with spin up and spin down. Evaluate the energy of this wavefunction using the full Hamiltonian including the electron-electron interactions. To determine the bond potential, change the distance between the atoms and recalculate the molecular orbitals for every distance. Construct the multielectron ground-state wavefunction for every distance and calculate its energy. This will give you an approximation of the bond potential.

(b) An N2 molecule can absorp light by making an electronic transition, a vibrational transition, or a rotational transition. To calculate the energies of the electronic transitions, construct a multielectron wavefunction of one of the excited states. This will be a Slater determinant using molecular orbitals which have a higher energy that the ground state. Evalaute the energy of this excited state using the full Hamiltonian. An N2 molecule can absorp photons with an energy $\hbar\omega= E_{\text{excited}}- E_{\text{ground}}$.

The vibrational levels can be found by solving the Schrödinger equation for a particle with a reduced mass $\mu = m_N/2$ moving in the bond potential that was calculated as described above. Here $m_N$ is the mass of a nitrogen atom. An approximate solution can be found by fitting the minimum of the bond potential with a parabola of the form $k(R-R_0)^2/2$ where $k$ is an effective spring constant. The vibrational energy levels are then given by,

\begin{equation} 
E_n=\hbar\omega(n+1/2) \hspace{1.5cm} n=0,1,2,\cdots, 
\end{equation}

where $\omega = \sqrt{k/\mu}$. An N2 molecule can absorp photons with an energy $\hbar\omega= E_m- E_n$ by making a vibrational transition from state $n$ to state $m$.

The rotational energies can be approximated using a rigid rotator model. The energies in this case are,

\begin{equation} 
 E_J= \frac{\hbar^2}{2I}J(J+1)\hspace{1.5cm} J=0,1,2,\cdots. 
\end{equation}

Here $I=\mu R_0^2$ is the the moment of inertia and $R_0$ is the interatomic distance that minimizes the bond potential. An N2 molecule can absorp photons with an energy $\hbar\omega= E_L- E_J$ by making a vibrational transition from state $J$ to state $L$.

Problem 2
A simple cubic crystal with lattice constant $a$ is cut so the (110) plane appears on the surface. The surface atoms form a two-dimensional crystal.

(a) What are the primitive lattice vectors of this two-dimensional crystal?

(b) Draw the Wigner-Seitz cell and the first Brillouin zone of the two-dimensional crystal. Label the size of of the unit cell and Brillouin zone in terms of $a$.

Problem 3
(a) Draw approximately the electron dispersion relation and the density of states for the one-dimensional potential, $V(x) = \cos\left(\frac{2\pi x}{a}\right)$ eV.

(b) There are 3 electrons per primitive unit cell, draw the position of the chemical potential in the plots of the dispersion relation and the density of states.

Problem 4
Silicon is doped with phosphorus (a donor) to a concentration of 10¹⁶ cm^-3. The temperature dependence of the electron density in the conduction band can be divided into three regimes: the freeze out regime, the extrinsic regime, and the intrinsic regime.

(a) Sketch a plot of the electron concentration in the conduction band as a function of temperature. Give formulas for the concentrations in the three regimes if you can.

(b) Approximately what temperature divides the freeze out regime from the extrinsic regime? Approximately what temperature separates the extrinsic regime from the intrinsic regime?

The donor level of phosphorus is 45 meV below the conduction band edge. The bandgap of silicon is 1.12 eV.

513.001 Molecular and Solid State Physics9.5.2014

Solution

513.001 Molecular and Solid State Physics
9.5.2014