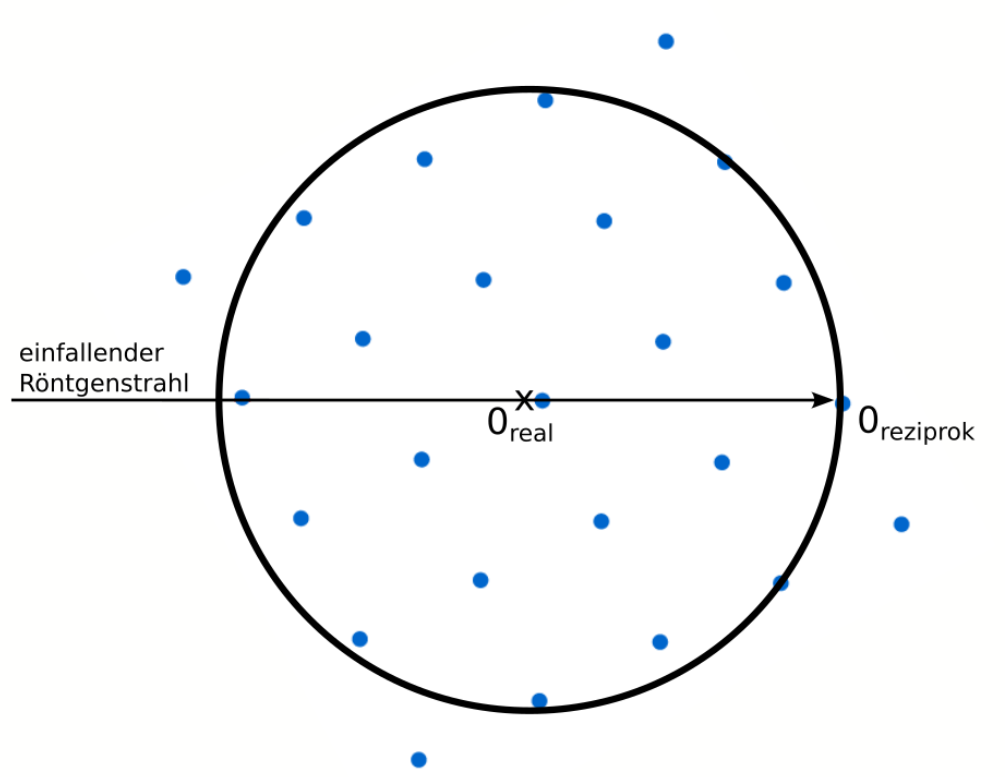
1. Diffraction
A tetragonal crystal has lattice constants $a=b=14.1$ Å, $c=6.8$ Å.
(a) Calculate the primitive reciprocal lattice vectors.
(b) In an x-ray diffraction experiment, x-rays with a wavelength of 6.28 Å are used. What is the Bragg angle for the (110) reflection?
(c) The drawing below shows the Ewald sphere drawn in the (001) plane. Include the primitive reciprocal lattice vectors, the reciprocal lattice vector $\vec{G}_{110}$ and the Bragg angle into this drawing.

Solution
2. Density of states
The density of a material is 8.96 g/cm³. The molar mass of the particles that make up the material is 63.5 g/mol. Every particle contributes one electron to the free electron density. 1 mole = $6.023 \times 10^{23}$ particles.
(a) Calculate the electron density of this material.
(b) Use the density of states given below to determine the Fermi energy of this material.
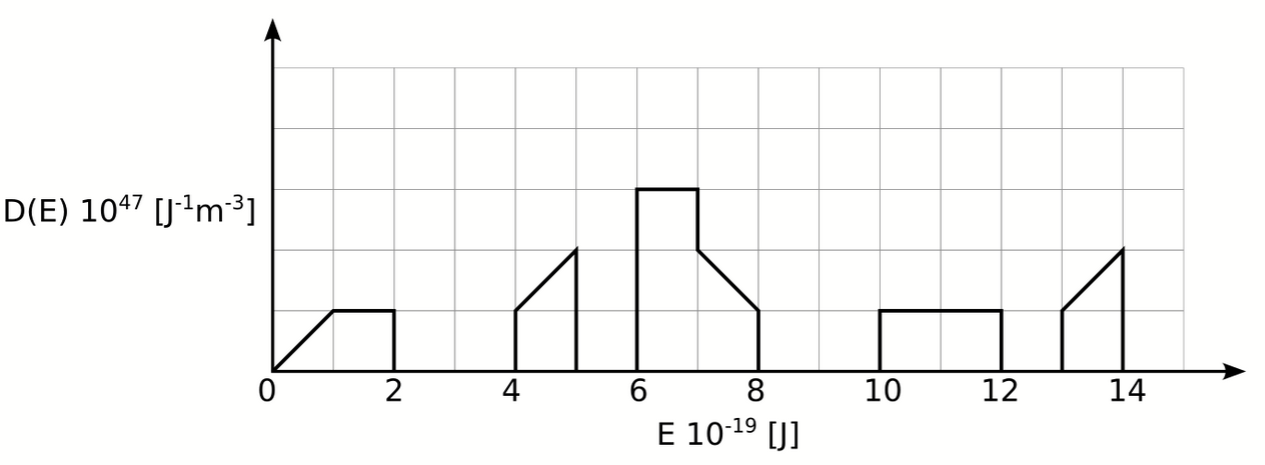
(c) Calculate the Fermi energy from the electron density using the Drude-Sommerfeld theory of a free electron gas.
(d) Is the assumption that the material can be described by the free electron model reasonable? Explain why or why not.
Solution
3. Thermal properties
The Fermi energy of a material is $E_F= 7.0$ eV. At low tempertures the specific heat of this material is linear with the temperature.
(a) At 30 K the heat capacity is measured to be 15 J mol-1 K-1. What is the heat capacity at 15 K?
(b) Is the heat capacity dominated by the electron contribution to the heat capacity or the phonon contribution to the heat capacity? Explain your reasoning.
Constants
$$\hbar = 1.05\times 10^{-34}\text{ Js}, \quad m_e = 9.11\times 10^{-31}\text{ kg}, \quad\ e = 1.60\times 10^{-19}\text{ C}, \quad\ k_B = 1.38\times 10^{-23}\text{ J/K}$$